Menu:

Phare de Chassiron sur l'île d'Oléron
Exercice 5.3 (Suite)
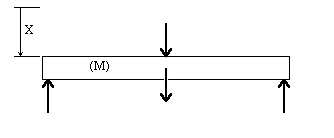
1- Sur la figure 3 de la dalle complète isolée, complétez les flèches en indiquant pour chacune d’elles la valeur de l’effort auquel elle correspond.
2- En utilisant le principe de la dynamique, montrez que l’équation de mouvement s’écrit sous la forme : $ M.x ↖{••} +2.K.x =M.g+F_0.\cosω.t $
3- Déterminez la pulsation propre $ω_0$ du système.
4- Déterminez la réponse $x_L(t)$ du système en vibrations libres.
5- Déterminez la réponse $x_F(t)$ du système en vibrations forcés.
6- En déduire la réponse globale du système $x(t)$.
A.N.:
$M=20000kg$, $K=3000N.m^{-1}$, $g=10N.m.s^{-2}$, $F_0=800N$
à t=0 : $x_0=0m$, $x↖{•}_0=0m.s^{-1}$