Menu:

Phare de Chassiron sur l'île d'Oléron
ou avec $k/{M+m}=ω_0^2$ et $b= m/{M+m} .a.ω_0^2.\sin ω.t$
$$ Y↖{••}+2.ε.ω_0.Y↖{•}+ω_0^2.Y= m/{M+m} .a.ω_0^2.\sin ω.t$$
a- Calcul du déplacement forcé par la méthode de FRESNEL
Cherchons Y sous la forme $Y=C.\sin (ω.t+φ)$
soit
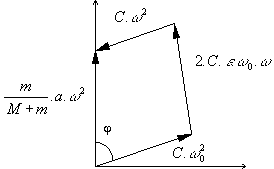
$ω_0^2.Y=ω_0^2.C.\sin (ω.t+φ)$ $2.ε.ω_0.Y↖{•}=2.ε.ω_0.C.\cos (ω.t-φ)=2.C.ε.ω_0.\cos (ω.t-φ+π/2)$ $Y↖{••}=-C.ω^2.\sin (ω.t-φ)=+C.ω^2.\sin (ω.t-φ+π)$
Par conséquent, nous obtenons : $$[C.(ω_0^2-ω^2)]^2+(2.C.ε.ω_0.ω)^2=(m/{M+m} .a.ω^2)^2$$
soit : $C={m/{M+m} .a.ω^2}/√{(ω_0^2-ω^2)^2+4.ε^2.ω_0^2.ω^2}$