

Menu:

Phare de Chassiron sur l'île d'Oléron
application : détermination de $ε$ quand $ε$ est faible:
$$Y_I/Y_{II}={e^{-ε.ω_0.T}}/{e^{{-ε.ω_0.(T+{2.π}/Ω_0})}}$$ $$=e^{ε.ω_0.{2.π}/Ω_0}$$ d’où $$ε={Ω_0}/{2.π.ω_0}.ln(Y_I/Y_{II})$$
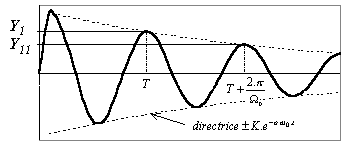
si $ε$ est supposé faible, on a : $Ω_0=ω_0. √{1-ε^2}≈ω_0$ $$ε=1/{2.π}.ln(Y_I/Y_{II})$$
222- Vibrations forcées dans le cas d’un machine déséquilibrée par un balourd
$$M.Y↖{••}+m.Y↖{••}+m.a.ω^2.\sin ω.t=-k.Y-b.Y↖{•}$$
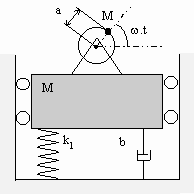
Ce système "excitateur à balourd" est principalement constitué par un rotor muni d’une surcharge et tournant à vitesse constante. Nous supposerons le moteur monté sur un socle pouvant seulement avoir un mouvement de translation verticale.
Le principe fondamental de la dynamique permet d’écrire l’équation du mouvement :
soit: $$(M+m).Y↖{••}+b.Y↖{•}+k.Y = -m.a.ω^2.\sin ω.t$$
En choisissant $Y>0$ lorsque le ressort s’allonge, nous obtenons de même: $$(M+m).Y↖{••}+b.Y↖{•}+k.Y = m.a.ω^2.\sin ω.t$$