

Menu:

Phare de Chassiron sur l'île d'Oléron
a- $Δ>O$ et $ε>1$ :(amortissement élevé)
$$α=-ε.ω_0 ± ω_0.√(ε^2-1)$$ soit: $Y_1=A_1.e^{-ε.ω_0.t}.e^{ω_0.√(ε^2-1).t}$ et$Y_2=A_2.e^{-ε.ω_0.t}.e^{-ω_0.√(ε^2-1).t}$
et $Y=Y_1+Y_2$ $$Y=e^{-ε.ω_0.t}.(A_1.e^{ω_0.√(ε^2-1).t}$$ $$+ A_2..e^{-ω_0.√(ε^2-1).t})$$
Le mouvement est dit "apériodique"

b- $Δ=O$ et $ε=1$ :(amortissement critique)
Dans ce cas, on montre que: $Y=e^{-ε.ω_0.t}.(B_1.t+ B_2)$
et que les allures des courbes de Y en fonction du temps sont identiques à celles obtenues pour un mouvement apériodique
c- $Δ<O$ et $ε<1$ :(amortissement faible)
$$α=-ε.ω_0 ± i. ω_0.√(ε^2-1)$$ $$=-ε.ω_0 ± i. Ω_0$$ $Ω_0$ est appelé la pseudo-période propre du système amorti. alors l’expression de Y peut se mettre sous la forme:
$$Y=e^{-ε.ω_0.t}.(C_1.\cos Ω_0.t$$$$+ C_2.\sin Ω_0.t)$$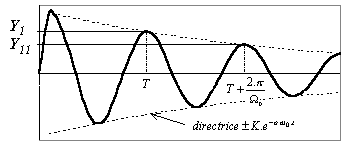
On obtient un mouvement "sinusoïdal amorti".