

Menu:

Phare de Chassiron sur l'île d'Oléron
22- Etude d’un système amorti (amortissement visqueux)
221- Vibrations libres
$$Y↖{••}+b/M.Y↖{•}+k/M.Y =0$$
Considérons le cas précédent de la fondation de machine. En appelant Y le déplacement de M par rapport à la position d’équilibre statique, nous avons l’équation du mouvement:
$-k.Y -b.Y↖{•}=M.Y↖{••}$ ,soit : $M.Y↖{••}+b.Y↖{•}+k.Y =0$ ou: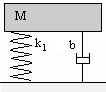
en posant: $k/M= ω_0^2$ et $b/M =2.ε.ω_0$
nous obtenons: $$Y↖{••}+2.ε.ω_0.Y↖{•}+ ω_0^2 .Y =0$$
Cherchons pour $Y$ une solution particulière de la forme:
$Y=A.e^{α.t}$ avec $α ∈ ℝ$
soit $Y↖{•}=α.A.e^{α.t}$ et $.Y↖{••}=^2.A.e^{α.t}$
par conséquent, l’équation étant satisfaite quel que soit t, on déduit: $$ α^2 +2.ε.ω_0.α+ ω_0^2=0$$
calculons: $Δ'=b'^2-4.a.c= ε^2.ω_0^2-ω_0^2 =ω_0^2.(ε^2-1)$