

Menu:

Phare de Chassiron sur l'île d'Oléron
De même pour un ressort de torsion de constante c, on obtient: $$ Ep = 1/2 .c.θ^2+cste $$
33- Principe de conservation de l’énergie
331- Hypothèse et énoncé
Hypothèse: Les forces extérieures agissant sur le système dérivent d’un potentiel; c’est à dire que l’énergie potentielle peut être calculée.
Soit un solide (S) soumis uniquement à une force $F↖{→}$ au point P. Le travail élémentaire $dW$ peut s’écrire:
$$ dW = F↖{→}.V↖{→}(G) + Ω↖{→}_s∧M↖{→}_{F↖{→}}(G) $$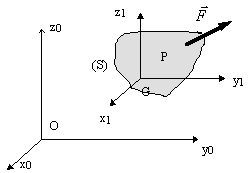
D’après le principe fondamental de la dynamique :
- $F↖{→}=M.γ↖{→}(G)=M.{dV↖{→}(G)/{dt}$
- $M↖{→}_{F↖{→}}(G)=δ↖{→}(G)={dσ↖{→}(G)}/{dt}={dI_{(G,(S), b_s)}.Ω↖{→}_s}/{dt} =I_{(G,(S), b_s)}.{dΩ↖{→}_s}/{dt} $
on introduit ces expressions dans l’ecriture de $dW$, on obtient:
$$ dW = M.V↖{→}(G).dV↖{→}(G) + Ω↖{→}_s . I_{(G,(S), b_s)}.dΩ↖{→}_s = M.V↖{→}(G).dV↖{→}(G) + I_{(G,(S), b_s)}.Ω↖{→}_s .dΩ↖{→}_s $$or $dW=-dEp$
Le premier terme $M.V↖{→}(G).dV↖{→}(G)$ représente $dEc$ de translation et le second terme $I_{(G,(S), b_s)}.Ω↖{→}_s .dΩ↖{→}_s $ représente $dEc$ de rotation.