Menu:

Phare de Chassiron sur l'île d'Oléron
32- Energie potentielle d’un système
321- Définition
Le calcul de l’expression du travail n’est pas toujours possible, en particulier lorsque le travail dépend de la trajectoire suivie pour passer d’un état initial à un état final, ou dans le cas du glissement.
Lorsque le travail dépend uniquement des positions initiales et finales, on dit que les forces correspondantes dérivent d’un potentiel et que le travail W est égal à l’opposée de la variation de l’énergie potentielle :
322- Exemples
a- Pesanteur
$ F↖{→}_{T_0} \{ \table 0 ; 0 ;-m.g$ et $ V↖{→}(P)_{T_0} \{ \table 0 ; 0 ;z↖{•}={dz}/{dt}$ $$ W = ∫ (F↖{→}.V↖{→}(P)).dt=-∫mg.dz =-m.g.∫_A^B dz $$ $$ Ep = m.g.z+cste $$
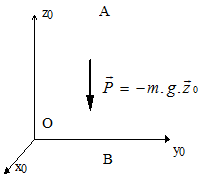
b- Ressort
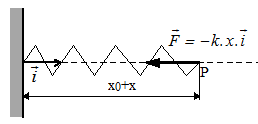
Pour un ressort linéaire de raideur k: $ F↖{→}=-k.x.i↖{→}$ et $ V↖{→}(P)={dx}/{dt} .i↖{→}$ $$ W = ∫ (F↖{→}.V↖{→}(P)).dt =k.∫_A^B x.dx $$ $$ W = 1/2 .k.(x_A^2-x_B^2)$$ $$ Ep = 1/2 .k.x^2+cste $$