

Menu:

Phare de Chassiron sur l'île d'Oléron
d- Vérifications à effectuer
il faut toujours vérifier les conditions suivantes:
- $N>0$, soit $M.g.\cos α >0$ et donc $π /2 > α >0 $
- $ T↖{→}$ et $U↖{→}_{DP}$ ce qui immédiat puisque $ T↖{→}$ et $U↖{→}_{DP}$ sont tous deux portés par le vecteur $i↖{→}_0$
- $T↖{→} . U↖{→}_{DP} ≤0$ soit $-f.M.g\cos α.[g.t.(\sin α-f.\cos α)-R. {2.f.g.t.\cos α}/R]$
soit après simplification: $f≤{\tan α}/3$
Nous pouvons remarquer que cette condition est complémentaire de celle trouvée dans l'hypothèse du roulement sans glissement.
En définitive la solution de ce problème varie suivant les valeurs respectives de $f$ et $α$.
si $$f>{\tan α}/3$$ alors $\{ \table {x↖{••}=2/3.g.\sin α};{θ↖{••}=-2/3.{g.\sin α}/R};{T=-{M.g.\sin α}/3};{N=M.g.\cos α}$ 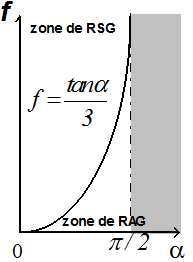
si $$f≤{\tan α}/3$$ alors $\{ \table {x↖{••}=g.(\sin α-f.\cos α)};{θ↖{••}={-2.f.g.\cos α}/R};{N=M.g.\cos α};{T=-f.M.g.\cos α}$