Menu:

Oleron Island Chassiron lighthouse

Phare de Chassiron sur l'île d'Oléron

 

  • $δ↖{→}(G)=d/{dt}[σ↖{→}(G)]$ or $σ↖{→}(G)=I_{(G,(S), b_s)}.Ω↖{→}_D = \[{\table {M.R^2}/4,0, 0 ; 0,{M.R^2}/4,0 ; 0,0,{M.R^2}/2}\].\[{\table 0 ; 0; θ↖{•}\] = {M.R^2}/2}.θ↖{•}.k↖{→}$

    • d’où: $δ↖{→}(G)={M.R^2}/2.θ↖{••}.k↖{→}$

    Soit l’expression du torseur dynamique de D: $$ \[ \table R↖{→}(γ)= M.x↖{••}.i↖{→}_0 ; δ↖{→}(G)={M.R^2}/2.θ↖{••}.k↖{→}$$

    222- Bilan des actions extérieures sur le solide
  • Pesanteur $$ \{ \table {R↖{→}_{P↖{→}}= M.g.(\sin α.i↖{→}_0 -\cos α.j↖{→}_0)} ;{ M↖{→}_{P↖{→}}(G)=0↖{→}}$$
  • Action de contact avec le sol $$ \{ \table {R↖{→}_A= T.i↖{→}_0 +N.j↖{→}_0)} ;{ M↖{→}_{R↖{→}_A}(I)=0↖{→}}$$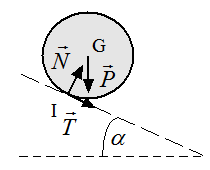
    		•
    $M↖{→}_{R↖{→}_A}(G)=M↖{→}_{R↖{→}_A}(I)+R↖{→}_A ∧{IG}↖{→}= (T.i↖{→}_0 +N.j↖{→}_0)∧R.j↖{→}_0 = T.R.k↖{→}_0 $

    Soit en définitive:

    • $R↖{→}_{Fe↖{→}}= (T+M.g.\sin α).i↖{→}_0 +(N-M.\cos α).j↖{→}_0$
    • $M↖{→}_{Fe↖{→}}(G)= T.R.k↖{→}_0 $