

Menu:

Phare de Chassiron sur l'île d'Oléron
On peut écrire:
$$σ↖{→}(O)=∫_S({OP}↖{→}∧.V↖{→}(P)).dm $$ $$=∫_S({OP}↖{→}∧[V↖{→}(G)+Ω↖{→}_s∧{GP}↖{→}]).dm $$ $$=∫_S({OP}↖{→}∧V↖{→}(G)).dm +∫_S({OP}↖{→}∧[Ω↖{→}_s∧{GP}↖{→}]).dm$$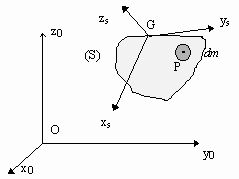
- Calcul du premier terme, en tenant compte de l'indépendance de G vis à vis du choix de l'élément d'intégration dm et de la définition du centre de gravité
$$∫_S({OP}↖{→}∧V↖{→}(G)).dm =(∫_S{OP}↖{→}.dm)∧V↖{→}(G)=M.{OG}↖{→}∧V↖{→}(G)$$ $$={OG}↖{→}∧M.V↖{→}(G)={OG}↖{→}∧R↖{→}(V)=R↖{→}(V)∧{GO}↖{→}$$- Calcul du second terme
On peut écrire: ${OP}↖{→}={OG}↖{→}+{GP}↖{→}.dm$ $$ ⇒ ∫_S({OP}↖{→}∧[Ω↖{→}_s∧{GP}↖{→}]).dm= ∫_S({OG}↖{→}∧[Ω↖{→}_s∧{GP}↖{→}]).dm+ ∫_S({GP}↖{→}∧[Ω↖{→}_s∧{GP}↖{→}]).dm$$
- $$ ⇒ ∫_S({OG}↖{→}∧[Ω↖{→}_s∧{GP}↖{→}]).dm={OG}↖{→}∧[Ω↖{→}_s∧∫_S{GP}↖{→}].dm= 0↖{→}$$
car ${OG}↖{→}$ et $Ω↖{→}$ sont indépendant de $dm$ et en tenant compte de la définition du centre de gravité
- $$ ⇒ ∫_S({GP}↖{→}∧[Ω↖{→}_s∧{GP}↖{→}]).dm = ?$$
soient: $Ω↖{→}_s_{(b_s)}=\[{\table p ; q ; r$ et ${GP}↖{→}_{(b_s)}=\[{\table x ; y ; z}$ On a alors: $Ω↖{→}_s∧{GP}↖{→}_{(b_s)}=\[{\table qz-ry ; rx-pz ; py-qx}$