

Menu:

Phare de Chassiron sur l'île d'Oléron
24- Transport des moments et produits d'inertie
241- Axes parallèles aux axes de bases et passant par G
2411- Moments d’inertie: Théorème des HUYGENS
${OP}↖{→}_{b_0}=\{\table x_0;y_0;z_0,,$ ${GP}↖{→}_{b_0}=\{\table x_1;y_1;z_1,$ , ${OG}↖{→}_{b_0}=\{\table a;b;c,,$ 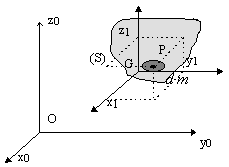
$$C_0=∫_S (x_0^2+y_0^2).dm$$ $$C_1=∫_S (x_1^2+y_1^2).dm$$ or : ${OP}↖{→}={OG}↖{→}+{GP}↖{→}=\{\table x_0=x_1+a;y_0=y_1+b;z_0=z_1+c,,$
d’où : $$C_0=∫_S (x_0^2+y_0^2).dm=∫_S ((x_1+a)^2+(y_1+b)^2).dm$$ $$=∫_S (x_1^2+a^2+2.a.x_1+y_1^2+b^2+2.b.y_1).dm$$ $$=∫_S (x_1^2+y_1^2).dm+2.a.∫_S x_1.dm+2.b.∫_S y_1.dm+(a^2+b^2).∫_S dm$$
car a et b sont des constantes indépendantes de $dm$ .
G est le centre de gravité de (S) d’où
$$∫_S {GP}↖{→}.dm=0↖{→} ⇨ \{ \table ∫_S x_1.dm =0;∫_S y_1.dm= 0$$