Menu:

Oleron Island Chassiron lighthouse

Phare de Chassiron sur l'île d'Oléron

 

    • par rapport aux plans de bases yOz, xOy, xOz
      • Plan yOz:     $d=x_P$    $$I_{yOz}=∫_S (x_p^2).dm$$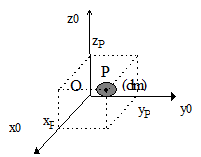
      Plan xOz: $d=y_P$ $$I_{xOz}=∫_S (y_p^2).dm$$
      Plan xOy: $d=z_P$ $$I_{xOy}=∫_S (z_p^2).dm$$

      Soit:

      $$I_O=I_{yOz}+I_{xOz}+I_{xOy}$$ $$I_O_x=I_{xOz}+I_{xOy}$$ $$I_O_y=I_{yOz}+I_{xOy}$$ $$I_O_z=I_{yOz}+I_{xOz}$$

23- Matrice d'inertie

Pour un système d'axes Ox, Oy, Oz, on définit la matrice d'inertie d'un solide en un point O sous la forme:

$$I_{(O,(S), b)}=\[{\table A,-F, -E ; -F,B,-D ; -E,-D,C}\]$$