Menu:

Oleron Island Chassiron lighthouse

Phare de Chassiron sur l'île d'Oléron

 

2- MOMENTS D'INERTIE ET PRODUITS D'INERTIE

  • Les produits d'inertie se définissent alors par:
    • $$D=∫_S y_P.z_P.dm$$
    • $$E=∫_S x_P.z_P.dm$$
    • $$F=∫_S x_P.y_P.dm$$
  • Expressions analytique des moments d'inertie
    • par rapport au point O:
    ${OP}↖{→}_{b_0}=\{\table x_P;y_P;z_P$   avec $$d = √{x_p^2+y_P^2+z_P^2}$$
    $$I_O=∫_S (x_p^2+y_P^2+z_P^2).dm$$
    • par rapport aux axes Ox, Oy, Oz

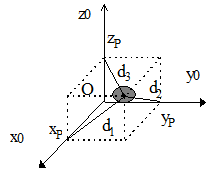
      • Axe Ox: $d_1 = √{y_P^2+z_P^2}$

      		$$I_O_x=A=∫_S (y_P^2+z_P^2).dm$$

      Axe Oy: $d_2 =√{x_p^2+z_P^2}$

      		$$I_O_y=B=∫_S (x_p^2+z_P^2).dm$$

      Axe Oz: $d_3 =√{x_p^2+y_P^2}$

      		$$I_O_z=C=∫_S (x_p^2+y_P^2).dm$$

      Soit:     $I_O={I_O_x+I_O_y+I_O_z} / 2$