

Menu:

Phare de Chassiron sur l'île d'Oléron
- Surfaces de révolution
Si Oz est l'axe de révolution, on a: $x_G = y_G=0$
L'élément de surface $ds$ se trouve entre les plans $dz-dz/2$ et $dz+dz/2$, $dz$ étant petit
$ds = 2.π.r.dl$ soit: $ S= ∫2.π.r.dl $ d'où:
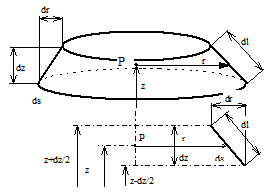
$ S.z_G= ∫z.ds =∫z.2.π.r.dl $
car $ds$ et $dl$ étant petit, on peut considérer que P, centre de gravité de $ds$ se trouve en $z_P=z$
- Volumes de révolution
De même, on aura:
$dv=π.r^2.dz$ soit:$ V= ∫π.r^2.dz $
d'où:
$ V.z_G= ∫z.dv =∫z.π.r^2.dz $
Remarque :
Il est nécessaire de transformer toutes les quantités en fonction de variables indépendantes avant de procéder à l'intégration