

Menu:

Phare de Chassiron sur l'île d'Oléron
- Surfaces planes définies sous forme polaire
On connaît la fonction donnant la limite de la surface $ρ=f(θ)$
l'élément $ds$ est assimilé à un triangle de base $ρ.dθ$, de hauteur $ρ$. On en déduit l'expression de $ds$ : $ds= 1/2 .ρ^2.dθ $ et donc
$$ S= 1/2 ∫_{θ_1}^{θ_2} ρ^2.dθ $$
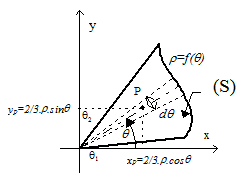
P est le centre de gravité de $ds$
$P \{ \table x_P=2/3.ρ.\cosθ;y_P=2/3.ρ.\sinθ$
d'où:
$$S.x_G=∫_{θ_1}^{θ_2} x_P.{ds}=1/3 .∫_{θ_1}^{θ_2} ρ^3(θ).\cosθ.dθ$$
$$S.y_G=∫_{θ_1}^{θ_2} y_P.{ds}=1/3 .∫_{θ_1}^{θ_2} ρ^3(θ).\sinθ.dθ$$