Soit une surface plane (S) tournant autour de l'axe Oy , ne le coupant pas. L'élément ds engendre un volume dv tel que: $$dv=ds.2.π.x_P$$ Le volume total engendré sera : $$V=2.π.∫_L{x_P.ds}=2.π.S.x_G$$

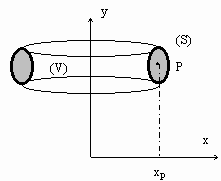
compte tenu de la définition du centre de gravité d'une surface matérielle.

Exemple : Centre de gravité d'une demi plaque circulaire.

$$V=2.π.S.x_G$$

$4/3 .π.R^3=2.π.{π.R^2}/2.x_G$    $ ⇨ $    $x_G={4.R}/{3.π}$

1232-Surfaces planes

Surfaces planes définies sous forme cartésienne On connaît $y_1(x)$ et $y_2(x)$ P est le centre de gravité de $ds$ $P \{ \table x_P;y_P={y_1(x)+y_2(x)}/2$
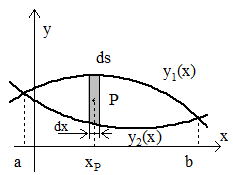
$ds=[y_1(x)-y_2(x)].dx$ d'où: $$S.x_G=∫_a^b x_P.{ds}$$	$$S=∫_a^b {ds}$$   $$S.y_G=∫_a^b y_P.{ds}$$