Menu:

Oleron Island Chassiron lighthouse

Phare de Chassiron sur l'île d'Oléron

 

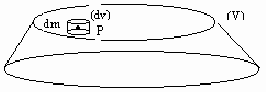
  • Volume matériel:

    • $$M.{OG}↖{→}=∫_s{{OP}↖{→}.dm}$$

    Pour un volume homogène, on a:

    $$V.{OG}↖{→}=∫_V{{OP}↖{→}.dv}$$
122- Simplifications éventuelles
  • Si un ensemble de masse M est composé de plusieurs solides de masse Mi, il est possible de trouver le centre de gravité G en concentrant les masses Mi aux centres de gravité Gi et en écrivant:

    • $$M.{OG}↖{→}= ∑↙{i=0}↖{i=n} M_i . {OG_i}↖{→}$$

  • Si un corps admet un plan, un axe ou un centre de symétrie, alors son centre de gravité se trouve dans ce plan, sur cet axe ou ce point.
123- Méthodes de calcul
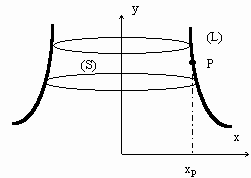
    1231- Théorèmes de GULDIN
  • Soit une courbe (L) tournant autour de l'axe Oy , ne le coupant pas. L'élément dl engendre une surface ds telle que:

    • $$ds=dl.2.π.x_P$$

    La surface totale engendrée sera :

    $$S=2.π.∫_L{x_P.dl}=2.π.L.x_G$$

    compte tenu de la définition du centre de gravité d'une ligne matérielle.