Menu:

Phare de Chassiron sur l'île d'Oléron
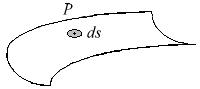
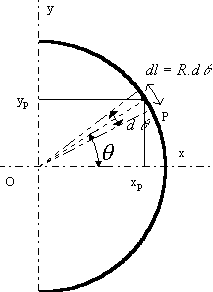
Exemple : demi-cerceau
$L=Π .R$ ${P\{\table x_P=R.\cosθ; x_P=R.\sinθ$
$$L.x_G↖{→}=∫_L{x_P.dl}=∫_{-Π/2}^{Π/2}{R.\cosθ.R.dθ}$$
$$=R^2∫_{-Π/2}^{Π/2}{\cosθ.dθ}=2.R^2$$
$$L.y_G↖{→}=∫_L{y_P.dl}=∫_{-Π/2}^{Π/2}{R.\sinθ.R.dθ}$$
$$=R^2∫_{-Π/2}^{Π/2}{\sinθ.dθ}=0$$
d’où: ${{OG}↖{→}\{\table x_G={2.R}/Π; y_G=0$
- Surface matérielle: (plaque, coque, ...)
$$M.{OG}↖{→}=∫_s{{OP}↖{→}}.dm$$
Pour une surface homogène, on a:
$$S.{OG}↖{→}=∫_S{{OP}↖{→}.ds}$$