EXERCICES DE DYNAMIQUE

EXERCICE 7-1:

Reprendre l'exercice 6-1:

e)- Calculer le torseur dynamique de (S) au point O

EXERCICE 7-2:

Reprendre l'exercice 6-2:

g)- Calculer le torseur dynamique de (S) en G

h)- Isoler le solide(S)

i)- Ecrire les équations découlant du principe fondamental de la dynamique.

EXERCICE 7-3:

On se propose d'étudier le mouvement d’un jouet d’enfant (J) constitué d’un manche assimilé à une tige (T) lié à un disque (D). La tige (T) de masse m de longueur L est lié au disque (D) de masse M de rayon R en son centre C par une liaison pivot d’axe Cz. Ce jouet se trouve posé sur un plan (P), incliné d’un angle fixe a par rapport à l’horizontale. L’extrémité A de la tige repose sur le plan.

I- ETUDE STATIQUE

On note f_i le coefficient de frottement entre le disque et le plan et f_a le coefficient de frottement entre la tige et le sol.

m=100 g, M=300g, R=15cm, L=60 cm, f_i=0,41 (j_i=22,5°).

1)- Faire un bilan des actions mécaniques extérieures agissant sur le jouet (J).

2)- Déterminer graphiquement la résultante des forces de pesanteur agissant sur (J).

3)- Déterminer graphiquement la valeur de l’angle de glissement j_a limite permettant l’équilibre du jouet sur le plan incliné.

4)- Cet équilibre est-il possible? (on rappelle que tg(45°)=1)

II- ETUDE DU MOUVEMENT

Dans cette partie, nous supposerons que le jouet se déplace le long du plan incliné. Nous supposerons qu’il y a roulement sans glissement en I entre le disque (D) et le plan (P) et glissement en A entre la tige (T) et le plan (P).

On repère les mouvements de (J) par les paramètres x et tels que:

Soit T₀ le repère de référence lié au plan (P), soit T₁ un repère mobile lié à (D) tel que .Soit T₂ un repère fixe lié à la tige (T) tel que AC est porté par Ax₂ et . On note .

Soit Oy, l'axe vertical ascendant de vecteur directeur .

Etude de la tige (T):

5)- Identifier la nature du mouvement de (T) et donner le vecteur rotation de la tige (T):

6)- A l'aide du théorème de huyghens, donner la matrice d'inertie de la tige (T) au point G_T dans b₂.

7)- Calculer le torseur cinétique de la tige au point C.

8)- Calculer le torseur dynamique de la tige au point C.

9)- Calculer l'énergie cinétique de la tige (T).

10)- Calculer l'énergie potentielle de la tige (T).

Etude du disque (D):

11)- Identifier la nature du mouvement de (D) et donner le vecteur rotation du disque (D): .

12)- Exprimer la condition de roulement sans glissement au point I.

13)- Calculer le torseur cinétique du disque (D) au point C.

14)- Calculer le torseur dynamique du disque (D) au point C.

15)- Calculer l'énergie cinétique du disque (D).

16)- Calculer l'énergie potentielle du disque (D).

Etude du solide (S):

Dans cette partie on supposera f_a connu.

17)- Calculer la position du centre de gravité G du jouet (J)

18)- Calculer le torseur dynamique du jouet (J) en C.

19)- Déduire des questions précédentes l'énergie cinétique du jouet (J).

20)- Déduire des questions précédentes l’énergie potentielle du jouet (J).

21)- Peut-on utiliser le théorème de l’énergie pour calculer le mouvement du jouet. Justifier la réponse.

22)- A l’aide de la question a)- donner le torseur au point C des actions extérieures agissant sur (J).

23)-En déduire les équations du principe fondamental de la dynamique appliqué au jouet (J).

Récupérez l'image ci-dessous et placer la au centre d'une feuille A4 pour traiter le problème graphiquement

schéma du jouet (J)

EXERCICE 7-4:

On considère un système constitué d'une tige (T) de masse m de longueur L et d'un disque (D) de centre C de masse 9.m de rayon L/3. La tige est articulée au point O par une liaison pivot d'axe Oz et est liée au disque par une liaison pivot en C d’axe Cz. Le disque est en contact permanent au point I avec un solide (S) immobile.

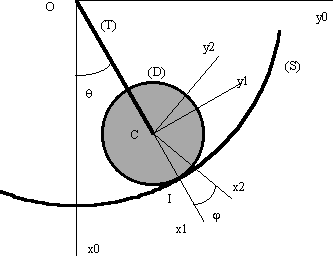
On repère les mouvements du système par les paramètres et j tels que:

Soit T₀ le repère de référence lié à (S), soit T₁ un repère mobile lié à (T) tel que . Soit T₂ un repère mobile lié au disque (D) tel que .

On supposera qu'il y a roulement sans glissement en I.

I- ETUDE DE LA TIGE

Soit G le centre de gravité de la tige (T).

1)- Calculez la vitesse de G.

2)- Donnez la matrice d'inertie de la tige (T) au point G dans b₁.

3)- Calculez le torseur cinétique de la tige au point G.

4)- Calculez le torseur dynamique de la tige au point C.

5)- Calculez l'énergie cinétique de la tige (T).

6)- Calculez l'énergie potentielle de la tige (T).

7)- Ecrire les équations découlant du PFD pour la tige (T).

II- ETUDE DU DISQUE

8)- Donnez la matrice d'inertie du disque (D) au point C dans b₂.

9)- Calculez le torseur cinétique du disque (D) au point C.

10)- Calculez l'énergie cinétique du disque (D).

11)- Calculez l'énergie potentielle du disque (D).

12)- Calculez le torseur dynamique du disque (D) au point C.

13)- Ecrire les équations découlant du PFD pour le disque (D).

14)- Donner l'équation de roulement sans glissement de (D) sur (S).

Mis à jour le: 05/12/05