EXERCICES DE CINETIQUE

EXERCICE 6-1:

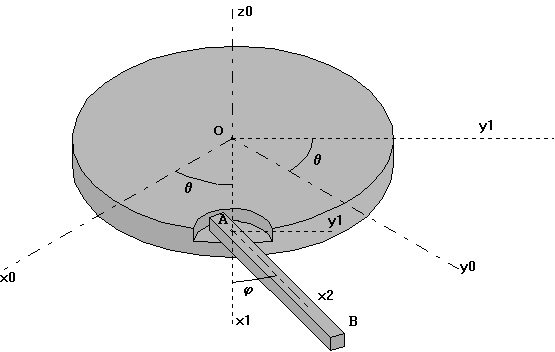
On considère un système constitué d'un disque (D) de masse M et d'une tige (T) de masse m. Le disque (D) tourne autour de l'axe et est repéré par angle de rotation q. La tige (T) lié au disque au point A tourne autour de et est repérée par angle de rotation j.

Soient les repères:
T₀ le repère de référence lié au sol
T₁ le repère lié au disque(D)
T₂ le repère lié à la tige (T)
On note:


On pose:
OA = R = constante
AB = L = constante
M=3.m et L=2.R

a)- Déterminer le torseur cinétique de (D) au point O

b)- Déterminer le torseur cinétique de (T) au point A

c)- En déduire le torseur cinétique de (S) au point O

d)- Déterminer l'énergie cinétique de (S)

EXERCICE 6-2:

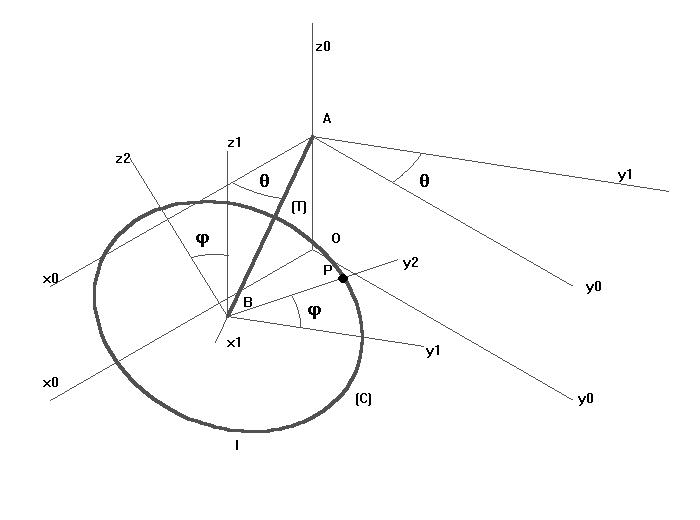
On considère un solide (S) constitué d'un cerceau homogène (C) de centre B, de masse M, de rayon R et d'une tige (T) de longueur AB=L de masse m en mouvement par rapport à un repère de référenceT₀ et soumis aux liaisons suivantes:

- (C) reste en contact en I avec le plan Ox₀y₀
- L'extrémité A de (T) est lié à l'axe Oz₀ par une liaison rotule
- La tige (T) reste parallèle au plan Ox₀y₀

Soient les repères:

T₀ le repère de référence lié au sol
T₁ le repère lié à la tige (T)
T₂ le repère lié au cerceau (C)

On note:			m=M

a)- Calculer la vitesse d'un point P du cerceau

b)- Exprimer la condition de roulement sans glissement du cerceau sur le plan Ox₀y₀

c)- Déterminer la position du centre de gravité G du solide (S)

d)- Déterminer la matrice d'inertie de (S) en G

e)- Calculer le torseur cinétique de (S) en G

f)- Calculer l'énergie cinétique de (S)

Mis à jour le: 11/02/04