

Menu:

Phare de Chassiron sur l'île d'Oléron
En cherchant $F_s$ sous la forme $F_S = F_{max}.\sin (ω.t-φ+ψ)$
il est possible d’établir un diagramme de FRESNEL correspondant Nous déduisons donc: $tan ψ={2.(M+m).C.ε.ω_0 .ω}/{(M+m).C.ω_0^2}$$={2.ε.ω_0}/{ω_0}=2.ε.r$
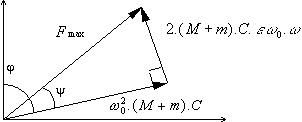
et $F_{max}^2=[ω_0 .(M+m).C]^2+[2.(M+m).C.ω_0 .ω]^2$
d’où :
$$F_{max}=(M+m).ω_0 ^2.C .√{1+4.ε^2.r^2}$$or $C=m/{M+m} . a.{r^2}/{√{(1-r^2)^2+4.ε^2.r^2}}$ et $r^2.ω_0 ^2 = ω^2$
d’où:
$$F_{max}= m.a.ω ^2.√{{1+4.ε^2.r^2}/{(1-r^2)^2+4.ε^2.r^2}}$$On en déduit le rapport de transmissibilité : $A_1 = F_{max}/{m.a.ω ^2}$
$$A_1= √{{1+4.ε^2.r^2}/{(1-r^2)^2+4.ε^2.r^2}}$$