

Menu:

Phare de Chassiron sur l'île d'Oléron
1- VIBRATIONS LIBRES NON AMORTIES D’UN SYSTEME A UN DEGRE DE LIBERTE
11- Equation du mouvement
Considérons un ensemble socle et machine de masse M, reposant sur un ressort élastique linéaire de raideur k, la surface du sol étant supposée infiniment rigide.
Appelons y le déplacement absolu du solide M.
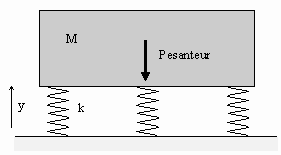
L’application du principe fondamental de la dynamique au système permet d’écrire
$$M.g-k.y=M.y↖{••}$$soit:
$$M.y↖{••}+k.y=M.g$$Cette relation peut également être établie à partir du principe de conservation de l’énergie.
12- Résolution de l’équation de mouvement
Posons: $y=Y+{M.g}/k$, le terme ${M.g}/k$représentant le déplacement "statique" du solide M.
Par conséquent: $y↖{••}=Y↖{••}$
D’où: $M.Y↖{••}-M.g+k.Y+M.g = 0$ ,soit : $M.Y↖{••}+k.Y =0$ ou: $$Y↖{••} + ω_0^2 .Y =0$$
avec : $ ω_0^2=k/M$