

Menu:

Phare de Chassiron sur l'île d'Oléron
Soit P’ la projection orthogonale du point P sur l’axe Δ
P’P est la distance de P à l’axe Δ d’où:
$$I_Δ = ∫_S \ov{P'P}^2 . dm$$ $ \ov {P'P}=∥u↖{→} ∧{OP}↖{→} ∥$ or $ u↖{→} ∧{OP}= ∣{\table α; β; γ}∧∣{\table x; y; z}=∣{\table β.z-γ.y; γ.x-α.z; α.y- β.x}$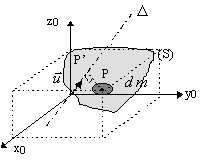
or :
$ \ov {P'P}^2=α^2.(y^2+z^2)+ β^2.(x^2.z^2)+ γ^2.(x^2+y^2) -2.β.γ.yz -2.α.γ.x.z -2α.β.x.y$
On obtient finalement:
$ I_Δ=[u↖{→}^t].[I_{(O,S,b)}].[u↖{→}]$
Ou sous forme matricielle:
$ I_Δ=α^2.A+ β^2.B+ γ^2.C -2.β.γ.D -2.α.γ.E -2α.β.F$
Remarques :
- On appelle axes principaux d’inertie, les axes pour lesquels les produits d’inertie sont nuls
- Dans le cas des surfaces planes, deux des produits d’inertie sont nuls. (ex: surface dans le plan Oxy: pour tous points P de la surface, z = 0 d’où D = E = 0)
- Dans le cas des solides de révolution, les axes perpendiculaires à l’axe de révolution jouent le même rôle. (ex volume de révolution autour de Oz: $I_{Ox}=I_{Oy}$ et $I_{xOz}=I_{yOz}$. D’après les relations vues précédemment, on en déduit que A = B = C/2)