

Menu:

Phare de Chassiron sur l'île d'Oléron
4- Cinématique du solide
Soit deux repères:
$T_0(O,i↖{→}_0, j↖{→}_0, k↖{→}_0)$ le repère de référence fixe
$T_1(O,i↖{→}_1, j↖{→}_1, k↖{→}_1)$ le repère mobile
Appelons $(x_1, y_1, z_1)$ les coordonnées d'un point P dans $(T_1)$; la relation vectorielle ${OP}↖{→}= {OO_1}↖{→} +{O_1P}↖{→}$ peut s'écrire ${OP}↖{→}= {OO_1}↖{→} +x_1 .i↖{→}_1+ y_1 .j↖{→}_1+z_1 . k↖{→}_1$
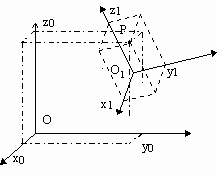
41- Calcul des vitesses
En dérivant l'expression du vecteur ${OP}↖{→}$ , nous obtenons:
${V}↖{→}_0(P)= {V}↖{→}_0(O_1) +x_1↖{•} .i↖{→}_1+x_1 .{di↖{→}_1}/{dt}+ y_1↖{•} .j↖{→}_1+ y_1 .{dj↖{→}_1}/{dt}+z_1↖{•} . k↖{→}_1+z_1 . {dk↖{→}_1}/{dt}$
soit:
${V}↖{→}_0(P)= ({V}↖{→}_0(O_1) +x_1 .{di↖{→}_1}/{dt}+ y_1 .{dj↖{→}_1}/{dt}+z_1 . {dk↖{→}_1}/{dt})+(x_1↖{•} .i↖{→}_1+ y_1↖{•} .j↖{→}_1+z_1↖{•} . k↖{→}_1)$
- Le terme (1) $({V}↖{→}_0(O_1) +x_1 .{di↖{→}_1}/{dt}+ y_1 .{dj↖{→}_1}/{dt}+z_1 . {dk↖{→}_1}/{dt})$ représente la vitesse qu'aurait le point P si ses coordonnées dans $(T_1)$ étaient constantes, c'est à dire si P était fixe par rapport à $(T_1)$. Ce terme représente la vitesse d'entraînement du point P . On la note: ${V}↖{→}_e(P)$.