

Menu:

Phare de Chassiron sur l'île d'Oléron
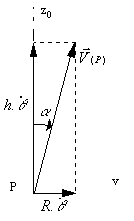
Cas particulier du mouvement hélicoïdal
- $ ρ=R=cste$ d'où on en déduit $ ρ↖{•}=ρ↖{••}=0$
- $z=h.θ$ , $h$ étant le pas de l'hélice.
${OP}↖{→}(P)= R.u↖{→}+ h.θ.k↖{→} $
${V}↖{→}(P)= R.θ↖{•}.v↖{→}+ h.θ↖{•}.k↖{→} $
$\tan α =R/h=cste$, le vecteur vitesse forme un angle constant avec la génératrice du cylindre sur lequel s’enroule l’hélice.
Si $ θ=ω.t+φ$, le mouvement est dit hélicoïdal uniforme
Cas particulier du mouvement plan
- $z=cste$ d'où on en déduit $ z↖{•}=z↖{••}=0$
${V}↖{→}(P)= ρ↖{•}.u↖{→} +ρ.θ↖{•}.v↖{→}$
ou $ ρ↖{•}.u↖{→}$ représente la vitesse radiale et $ρ.θ↖{•}.v↖{→}$ la vitesse orthoradiale.
${γ}↖{→}(P)=(ρ↖{••}-ρ.θ↖{•}^2).u↖{→} +(2.ρ↖{•}.θ↖{•}+ρ.θ↖{••}).v↖{→} $
avec $ (ρ↖{••}-ρ.θ↖{•}^2).u↖{→}$ l'accélération radiale et $(2.ρ↖{•}.θ↖{•}+ρ.θ↖{••}).v↖{→}$ l'accélération orthoradiale.