Menu:

Phare de l'île d'Aix
d'où :
- $C_{Ω_2\\Ω_1}=2.F+E$
- $X_A={√3/2}.(2.F+E)$
- $Y_A=E/2$
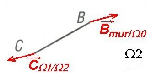
Revenons au solide $Ω_2$
Figure 4.11: Solide $Ω_2$ isolé
$B↖{→}_{mur\\Ω_0}=-C↖{→}_{Ω_1\\Ω_2}$
- en projection sur $x$ : $X_B=-C_{Ω_2\\Ω_1}.\cos30°$ soit : $X_B={√3}.(F+E/2)$
- en projection sur $y$ : $Y_B=-C_{Ω_2\\Ω_1}.\sin30°$ soit : $Y_B=F+E/2$
- De plus : $C↖{→}_{Ω_1\\Ω_2}=N_{BC}.x↖{→}_{BC}$ soit : $N_{BC}=2.F+E$
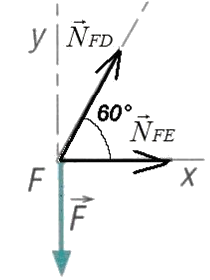
Isolons le noeud F : d'après le principe de la statique
Figure 4.12: Noeud F isolé
$N↖{→}_{FE}+N↖{→}_{FD}+F↖{→}=0↖{→}$
d'ou :
- en projection sur $Fx$ :
$N_{FE}+N_{FD}.\cos60°=0$
- en projection sur $Fy$ :
$N_{FD}.\sin60° -F=0$
$N_{FD}={{2.√3}/3}.F$ $N_{FE}={{-√3}/3}.F$