L'objectif de ce chapitre est de rappeler succintement les notions mathématiques nécessaires à la compréhension de la suite de ce cours.
Chap .1: RAPPELS DE CALCULS
![]()
2-
OPERATIONS SUR LES VECTEURS
![]()
![]()
![]()
![]()
· E® R · ®
Dans une base ![]() , si
, si ![]() et
et ![]() , alors on
aura
, alors on
aura
| Remarque: · Le résultat du produit scalaire de deux vecteurs est un SCALAIRE. |
· Propriétés:
· Commutativité:![]()
· Distributivité à droite et à gauche:![]() et
et ![]()
· Multiplication par un réel:![]()
· Normes:![]()
· Calculs sur les vecteurs d'une base orthonormée directe:
![]()
![]()
· E² ® E · ®
Dans une base ![]() , si
, si ![]() et
et ![]() , alors on
aura
, alors on
aura
· Méthode de calcul:
Calcul à effectuer: 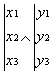
Première composante: On barre la première ligne et on calcule le déterminant 2*2 restant:
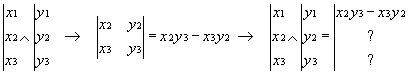
Deuxième composante: On barre la deuxième ligne et on calcule l'opposé du déterminant 2*2 restant:
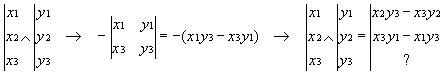
Troisième composante: On barre la troisième ligne et on calcule le déterminant 2*2 restant:
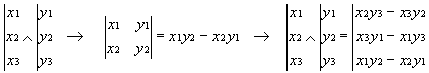
| Remarque: · Le résultat du produit vectoriel de deux vecteurs est un VECTEUR perpendiculaire aux deux vecteurs . |
· Propriétés:
· Anticommutativité:![]()
· Distributivité à droite et à gauche:![]() et
et ![]()
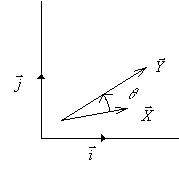
· Multiplication par un réel:![]()
| · Calcul pratique du produit
vectoriel: si
on définit l'angle |
· Calculs sur les vecteurs d'une base orthonormée directe:
![]() ,
, ![]() ,
, ![]()
![]()
· E3 ® R · ®
| Remarque: · Le résultat du produit mixte de trois vecteurs est un SCALAIRE. |
· Propriétés:
· ![]() si l'un des vecteurs est une combinaison linéaire
des deux autres.
si l'un des vecteurs est une combinaison linéaire
des deux autres.
· ![]()
Un torseur est un champ de
vecteurs, antisymétrique de E. Un torseur ![]() en un point
en un point ![]() est défini par:
est défini par:
· Un vecteur libre appelé Résultante du torseur
· Un vecteur dépendant du point A ou il est exprimé appelé Moment du torseur en A et vérifiant:
| Remarque: · La résultante du torseur est indépendante du point où est défini un torseur. |
32-
Application des torseurs à la représentation d'un champ de
force
![]()
![]()
![]()
![]()
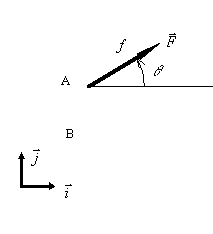
Soit un champ de force défini
dans l'espace à trois dimensions de base orthonormée directe![]() par la
donnée de la force
par la
donnée de la force ![]() appliquée en un point
appliquée en un point ![]() :
:
![]() ou
ou ![]()
Le moment de la force ![]() en son point
d'application
en son point
d'application ![]() est nul d'où:
est nul d'où: ![]() .Si on veut calculer le moment de la force
.Si on veut calculer le moment de la force
![]() au point
au point
![]() , on
obtient
, on
obtient ![]() (intensité de la force
(intensité de la force ![]() multiplié par le bras de levier
multiplié par le bras de levier ![]() , sens
négatif).
, sens
négatif).
En appliquant la notion de
torseur, on peut définir le torseur force ![]() au point A,
associé à
au point A,
associé à ![]() par:
par:
· la résultante du torseur force
égale à la force
· le moment en
du torseur force
égal à
Le moment au point ![]() est défini
par la formule de transport donnée plus haut soit:
est défini
par la formule de transport donnée plus haut soit:
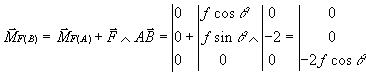
ou:
| Remarques: · La notion de torseur de force permet donc de parler globalement d'une force et de son moment en tout point de l'espace. · Les deux vecteurs définis dans un torseur sont de natures différentes. Pour un torseur de force, le vecteur résultant est une force ayant des composantes dont les unités sont des (N), alors que le moment en un point est un moment dont les composantes ont des unités en (N.m). · Attention quand l'on demande de définir un torseur , il est nécessaire de donner une réponse pour la résultante et une réponse pour le moment. |
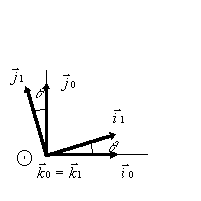
Soient deux bases orthonormées directes
| 
|
41-
Projection des vecteurs de bases
![]()
![]()
![]()
![]()
![]()
Si on exprime les vecteurs de la
base![]() dans
dans ![]() ,
on obtient:
,
on obtient:
·
·
·
Inversement, si on exprime les
vecteurs de la base ![]() dans
dans ![]() , on obtient:
, on obtient:
·
·
·
42-
Changements de bases d'un vecteur quelconque
![]()
![]()
![]()
![]()
Soit ![]() un vecteur
exprimé dans la base
un vecteur
exprimé dans la base ![]() . L'expression de
. L'expression de ![]() dans la base
dans la base ![]() sera:
sera:
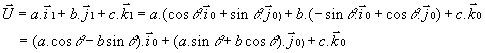
d'où:
| · |
· |
| · |
· |
| · |
· |
| · |
· |
| · |
· |
| · |
· |
![]()
Mis à jour le: 11/02/04
![]()