

Menu:

Phare de Chassiron sur l'île d'Oléron
2- Notions de mouvement et de repos - Repères absolu et relatif - Repères de référence et de projection
Un point P est dit en mouvement par rapport à un repère si au moins une de ses coordonnées varie en fonction du temps. Si toutes ses coordonnées restent constantes, on dit qu'il est au repos par rapport à ce repère.
Cette notion est relative: un voyageur assis dans un train est en mouvement par rapport à un repère lié à la terre et est au repos par rapport à un repère lié au train.
Dans la suite de ce cours, nous appellerons $(T_0)$ le repère absolu ou de référence supposé fixe et $(T_1)$ le repère mobile. Les bases associées à ces repères seront toujours orthonormées directes.
On appelle mouvement d'entraînement le mouvement permettant de passer de $(T_0)$ à $(T_1)$.
Examinons maintenant la différence entre repère de référence et repère de projection.
Pour cela, considérons l'exemple d'un mouvement circulaire uniforme ($ω$ constante).
Dans ce cas, on sait que la vitesse est tangente au cercle et que son module est $R.ω$. Le repère de référence est $(T_0)$ et $R.ω$ représente la vitesse par rapport à ce repère. On peut exprimer les composantes du vecteur vitesse dans $(T_0)$, mais il est plus facile de les exprimer dans le repère mobile $(T_1)$, en effet on a simplement ${V(P)}↖{→}=R.ω.j↖{→}_1$ .
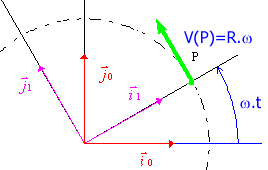
On a alors exprimé la vitesse du point P par rapport à $(T_0)$ en exprimant ses composantes dans un autre repère $(T_1)$. $(T_0)$ est le repère de référence tandis que $(T_1)$ est le repère de projection.