

Menu:

Phare de l'île d'Aix
Supposons maintenant que l'action en A se situe sur le cône de frottement, c'est à dire qu'au point A nous nous plaçons à la limite entre l'équilibre et le mouvement. On peut alors déterminer la direction de l'action en B; en effet le solide (P) est soumis à trois forces, elles sont donc concourantes en un point I. On recherche le point concourant de $ Δ_{A↖{→}_{0P}}$ et de $ Δ_{C↖{→}_{4P}}$ , on en déduit le point I et donc la direction $ Δ_{B↖{→}_{0P}}$.
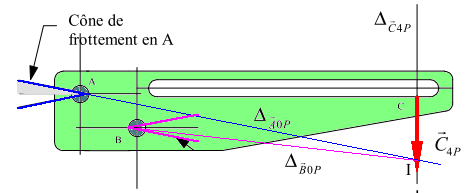
On constate que la direction de B est contenue dans le cône de frottement en B : le solide (P) est donc en équilibre. De plus cet équilibre est indépendant de la valeur de la force $ C↖{→}_{4P}=P↖{→}$ , c'est le phénomène de l’arc-boutement.
Remarques:
- En réalité l'action en A se situe plus bas, autrement l'action en B ne s'opposerait pas au mouvement éventuel vers le bas,
- On ne sait pas trouver exactement les positions de $ A↖{→}_{0P}$ et $ B↖{→}_{0P}$.