Menu:

Phare de l'île d'Aix
Bilan des actions extérieures exercées sur le solide (P)=(1+2+3):
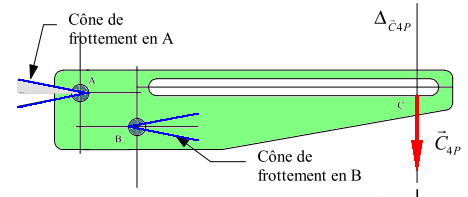
- Action de l'axe (4) en C: $[C_{4P}]_C ⇒ C↖{→}_{4P} = P↖{→}$ et $M↖{→}_{C↖{→}_{4P}}(C) = 0↖{→}$
- Action de la tige (0) en A avec frottement:
$[A_{0P}]_A ⇒ A↖{→}_{0P} $ inconnue et $M↖{→}_{A↖{→}_{0P}}(A) = 0↖{→}$
- Action de la tige (0) en B avec frottement:
$[B_{0P}]_B ⇒ B↖{→}_{0P} $ inconnue et $M↖{→}_{B↖{→}_{0P}}(B) = 0↖{→}$
On dispose ici de quatre inconnues, modules et directions de $A↖{→}_{0P}$ et $B↖{→}_{0P}$ et de trois équations (le système est plan); le système est hyperstatique de degré 1. Toutefois nous allons pouvoir malgré tout analyser son comportement.
Connaissant les coefficients de frottement en A et B, nous connaissons les angles de frottement en A et B. Les actions $A↖{→}_{0P}$ et $B↖{→}_{0P}$ sont toujours contenues dans les cônes de frottement. De plus, nous savons que les actions en A et B s'opposeront à un éventuel mouvement. On peut donc en déduire que l'action en A se situera dans la zone grisée sur le schéma ci dessous.