EXERCICES DE CINEMATIQUE

EXERCICE 4-1:

Soit un point M de coordonnées dans un repère

a)- Calculez les coordonnées cylindriques de M.

b)- Calculez les coordonnées sphériques de M.

Pour chaque question donnez une représentation.

EXERCICE 4-2:

On considère un point M de coordonnées dans un repère T

x = a.cos(w t)

y = a.sin(w t)

z = b.t

a)- a et b sont des constantes
	a.1)- Déterminez la vitesse du point M
	a.2)- Déterminez l'accélération du point M
	a.3)- Déterminez la trajectoire du point M
b)- On pose a = z.tgq , b et q sont des constantes
	b.1)- Déterminez la vitesse du point M
	b.2)- Déterminez l'accélération du point M
	b.3)- Déterminez la trajectoire du point M

EXERCICE 4-3:

Soit un repère To lié à la terre de base b₀

a)- Une cible C ayant pour accélération à tout instant part du point à un instant initial t_i avec une vitesse de module V₀ et faisant un angle a avec l'axe 0x:

a.1)- Déterminez les composantes de
a.2)- Calculez l'altitude maximale atteinte par la cible
a.3)- Calculez à quelle distance du point A la cible va atterrir
a.4)- A.N.:

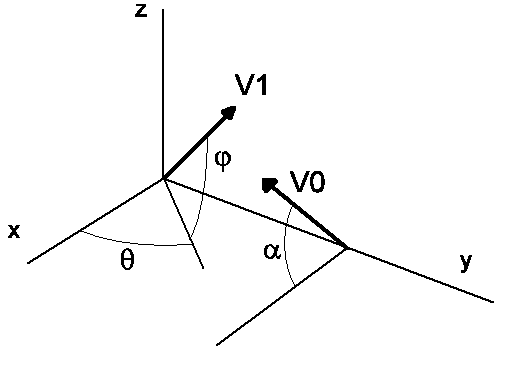
b)- Un canon placé au point O lance un projectile destiné à atteindre la cible. Le canon est orienté suivant la direction d'un vecteur dans le plan oxy et tel que . Le projectile partira à un instant t'_i avec une vitesse de V₁et faisant un angle j avec le vecteur .Soit T₁le repère de base b1.

b.1)- Déterminez les composantes de et de exprimés dans b₁
b.2)- En déduire les composantes de et de exprimés dans b₀
b.3)- Si t'_i = t_i ,déterminez les angles q et j pour atteindre la cible à son altitude maximale.
b.4)- Quelle doit être alors la vitesse du projectile ?
b.5)- A.N.:

EXERCICE 4-4:

On considère les repères To, T₁,T₂ tels que et . Un point M est tel que , avec R=constante.

a)- Donnez les expressions de et dans b₁

b)- Donnez les expressions de et dans b₀

c)- Donnez les coordonnées cartésiennes du point M dans b₀

d)- Donnez les expressions de la vitesse et de l'accélération du point M par rapport au repère de référence T₀

e)- Donnez les expressions de la vitesse et de l'accélération du point M par rapport au repère de référence T₁

EXERCICE 4-5:

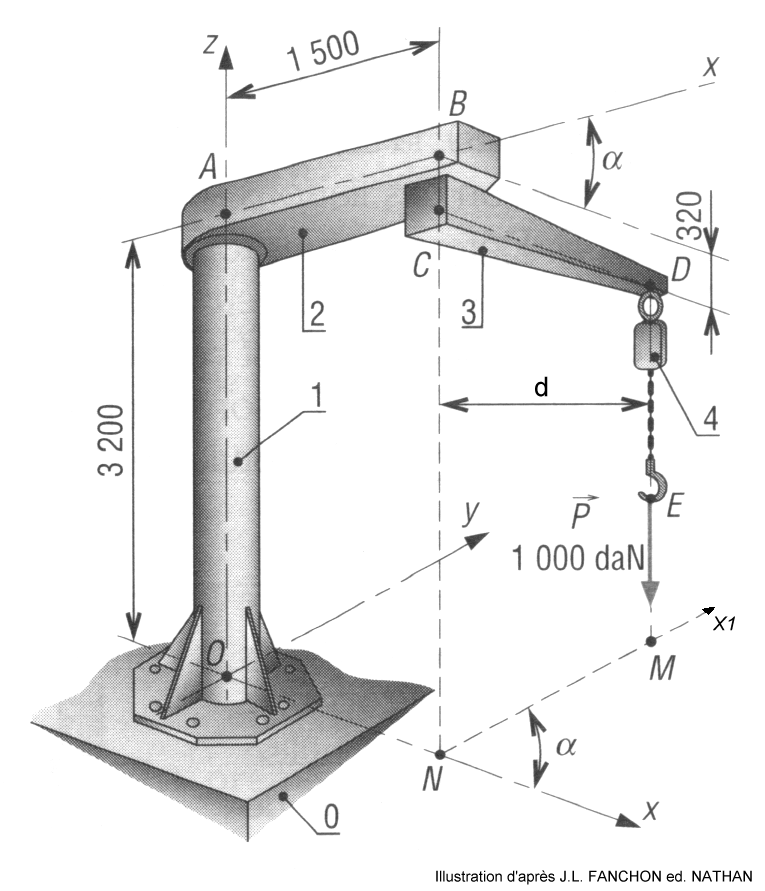
On considère une potence de manutention représentée

Le corps (1) de la potence est fixé au sol (0) par une liaison encastrement. La tête (2) est encastrée au point A sur le corps (1). Au point C de (2), une liaison pivot d’axe Cz permet au bras (3) de tourner autour de l’axe vertical. L’axe de symétrie du bras (3) définit ainsi une axe mobile Cx₁. On notera . Le palan (4) est accroché au point D sur le bras (3) par une liaison glissière d’axe Cx₁ On notera , d (variable). Enfin la charge située au point E peut monter ou descendre suivant l’axe Dz. On notera , h (variable). Le poids de la potence est négligeable devant la charge .

1) Déterminez par une étude analytique les actions exercées par le corps de la potence (1) sur le sol (0) au point O.

2)Calculez l’expression de la vitesse du point E par rapport au repère fixe To.

3)Calculez l’expression de l’accélération du point E par rapport au repère fixe To

EXERCICE 4-6:

On considère un manège symbolisé par un cerceau de centre O et de rayon R tournant autour de son axe à la vitesse angulaire w . En un point A du cerceau est suspendue une nacelle par une liaison pivot d'axe .Soit B un point de la nacelle tel que

a)- Déterminez la vitesse et l'accélération du point B.

EXERCICE 4-7:

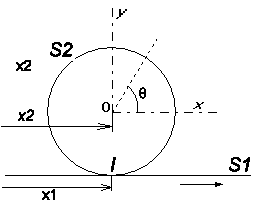
On considère un disque S₂ en mouvement sur un plan S₁. A l'instant t, le disque est en contact avec le plan S₁ au point I de l'espace. soit I₁ et I₂ les points respectifs du plan et du disque en contact à cet instant. Le disque tourne autour de l'axe et est repéré par la position x₂ de son centre ainsi que son angle de rotation q . Le plan S₁ se déplace en translation et la poisition du point I₁ est repérée par le paramètre x₁.

Soient les repères:

T₀ le repère de référence lié au sol