EULER Léonard
![]()
(1707 - 1783)
| Avec Joseph-Louis Lagrange, son émule plus jeune, Leonhard Euler est l’un des deux géants mathématiques qui ont dominé la science du XVIIIe siècle. Ses travaux, d’une abondance inégalée, couvrent tout le champ des mathématiques, de la mécanique céleste et de la physique de son époque. Il a renouvelé l’articulation entre les secteurs mathématiques, fixé la plupart des notations du calcul infinitésimal que nous utilisons encore, développé la théorie des nombres de Fermat et systématisé la géométrie analytique de Descartes tout en l’étendant du plan à l’espace; en mécanique et en élasticité, il a été le premier à pouvoir utiliser les développements contemporains de l’analyse (dont beaucoup lui étaient dus) en les conjuguant avec les principes de la physique newtonienne sur des bases théoriques solides. |  |
Éléments biographiques
Né à Bâle d’un père pasteur, Paul Euler (1670-1745), qui avait étudié les mathématiques avec Jacques Bernoulli, le jeune Leonhard Euler, que son père destinait au ministère religieux, reçut une éducation très complète en théologie, langues orientales, médecine, physique, astronomie et mathématiques; il étudia cette dernière science avec Jean Bernoulli et se lia d’amitié avec les deux fils, Nicolas et Daniel, de son maître. En 1727, il fut attiré à Saint-Pétersbourg par Nicolas et Daniel Bernoulli, pour siéger à l’Académie que l’impératrice Catherine 1re venait de fonder en 1725; un poste lui était offert dans la section de médecine et de physiologie. En 1730, il obtenait un poste en philosophie naturelle; après la mort de Nicolas et le départ pour Bâle de Daniel Bernoulli en 1733, Euler se trouvait le principal mathématicien à Saint-Pétersbourg: il était déjà connu pour de nombreux ouvrages, dont un avait été primé par l’Académie des sciences de Paris en 1724 (sur la théorie des marées, prix partagé avec C.Maclaurin et D.Bernoulli). La perte de son œil droit en 1735 ne diminua pas son intense activité scientifique. À l’appel de Frédéric II, il se rendit à Berlin en 1741 pour faire partie de l’Académie de cette ville; il n’y fut pas estimé à sa juste valeur et préféra retourner à Saint-Pétersbourg en 1766, année où il ressentit les premiers symptômes de la cataracte qui devait lui ôter l’usage de son œil gauche, malgré une opération en 1771, et le rendre aveugle pour les dix-sept dernières années de sa vie. Sa cécité ne l’empêcha pas de continuer à travailler et à rédiger des mémoires qu’il dictait à des personnes de son entourage. Il mourut subitement en 1783, laissant derrière lui une œuvre scientifique d’une ampleur inégalée, dont le catalogue (établi par G. Eneström en 1910-1913) ne comporte pas moins de 886 titres; ses œuvres complètes comprennent près de quatre-vingts volumes.
Mathématiques
Euler est l’auteur de trois grands traités didactiques sur l’analyse infinitésimale, dans lesquels il a exposé sa conception nouvelle du calcul différentiel et intégral et ses rapports avec la géométrie: l’Introductio in analysin infinitorum 1748), les Institutiones calculi differentialis (1755) et les Institutiones calculi integralis (3 vol., 1768-1770). Le premier de ces traités opère une refonte dans le mode d’exposition de ces questions: il met au premier plan le concept de fonction, défini de façon formelle comme "une expression analytique composée d’une manière quelconque d’une quantité variable et de nombres ou de quantités constantes". Cette définition reprend celle que Jean Bernoulli avait déjà donnée (le terme avait été introduit par Leibniz); l’originalité d’Euler tient dans le rôle fondamental qu’il fait jouer à ce concept, qui n’était que marginal avant lui. Le premier livre de l’Introductio est consacré au calcul "algébrique" sur les fonctions, étant entendu qu’Euler considère encore comme algébriques les procédures infinies qui étendent les opérations usuelles: séries et produits infinis, fractions continues; au second livre, il applique les méthodes et les résultats du premier livre à des problèmes de géométrie (étude des courbes algébriques ou transcendantes, surfaces, changements d’axes de coordonnées). Il y a là un renversement très important par rapport aux traités antérieurs dans lesquels le calcul était au contraire tributaire de la géométrie. Euler donne dans l’Introductio ( chap. VI à VIII) un exposé des fonctions transcendantes élémentaires: la fonction exponentielle, le logarithme et les fonctions trigonométriques, qui sont envisagées ainsi pour la première fois. L’exponentielle az (où a>0 est une constante) est définie par interpolation pour z réel, entre les valeurs rationnelles de z, et le logarithme est défini comme fonction inverse de l’exponentielle (ce qui est nouveau); les fonctions circulaires sin et cos sont, pour la première fois, considérées comme des fonctions d’une variable réelle (ou même complexe) et non plus comme des liges qui dépendent d’un angle; elles sont liées à l’exponentielle par les célèbres formules d’Euler:
![]() et
et ![]()
où se trouvent le nombre e, base des
logarithmes népériens (la notation e pour ce nombre est
due à Euler, qui l’employait depuis 1728), et l’unité
imaginaire ![]() ,
notée ici i comme Euler l’a fait plus tard, en 1777.
Un autre nombre célèbre, le rapport de la circonférence au
diamètre, avait été noté p par W.Jones en 1706, mais
c’est Euler qui a imposé cette notation à l’usage des
mathématiciens; il est lié aux précédents par la célèbre
formule eip =-1 écrite par Euler. Cette
formule attribue le logarithme imaginaire ip au nombre -1,
contrairement à ceux qui croyaient pouvoir déduire de
l’égalité lg(-1)2= lg(+1)2 celle des
logarithmes de 1 et de -1. Le paradoxe précédent avait été
résolu par Euler, qui avait montré que chaque nombre (réel ou
complexe) a une infinité de logarithmes qui diffèrent entre eux
par un multiple entier arbitraire de 2ip; dans le cas
d’un nombre réel positif, un seul des logarithmes a une
valeur réelle. À propos des logarithmes, Euler remarque que,
lorsque a et b sont rationnels, lgab
n’est ni rationnel (sauf si b est une puissance
entière de a), ni la racine carrée d’un nombre
rationnel; c’est la base du septième problème de Hilbert,
résolu en 1934 par Gelfond et Schneider.
,
notée ici i comme Euler l’a fait plus tard, en 1777.
Un autre nombre célèbre, le rapport de la circonférence au
diamètre, avait été noté p par W.Jones en 1706, mais
c’est Euler qui a imposé cette notation à l’usage des
mathématiciens; il est lié aux précédents par la célèbre
formule eip =-1 écrite par Euler. Cette
formule attribue le logarithme imaginaire ip au nombre -1,
contrairement à ceux qui croyaient pouvoir déduire de
l’égalité lg(-1)2= lg(+1)2 celle des
logarithmes de 1 et de -1. Le paradoxe précédent avait été
résolu par Euler, qui avait montré que chaque nombre (réel ou
complexe) a une infinité de logarithmes qui diffèrent entre eux
par un multiple entier arbitraire de 2ip; dans le cas
d’un nombre réel positif, un seul des logarithmes a une
valeur réelle. À propos des logarithmes, Euler remarque que,
lorsque a et b sont rationnels, lgab
n’est ni rationnel (sauf si b est une puissance
entière de a), ni la racine carrée d’un nombre
rationnel; c’est la base du septième problème de Hilbert,
résolu en 1934 par Gelfond et Schneider.
Euler était exceptionnellement doué pour le calcul, aussi bien numérique que formel. Dans l’Introductio, il manipule les séries et les produits infinis d’une façon prodigieuse et il trouve des résultats très remarquables, comme le développement de sin z en produit infini:
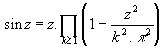
qui lui donne les sommes des séries:
![]()
sous la formeAn.p2n,
avec An rationnel, dont Euler donne la
valeur numérique pour 1£ n£ 13. Le cas n=1
était un problème célèbre, qui avait résisté à Jacques
Bernoulli, et dont Euler avait communiqué la solution à
D.Bernoulli vers 1736; dans le cas général, Euler a découvert
plus tard le lien entre les coefficients An
et les nombres de Bernoulli (Institutiones calculi
differentialis, 2e part., chap.V). Il avait aussi calculé
les valeurs numériques de:![]()
pour 1£ n£ 5, et leurs rapports respectifs à p2n+1, sans y reconnaître des nombres rationnels remarquables; on sait depuis (Apéry, 1978) que z(3) est un nombre irrationnel, mais on n’en sait pas plus. Les nombres de Bernoulli apparaissent aussi dans la formule sommatoire découverte par Euler en 1732-1735 et, indépendamment, par Maclaurin, qui donne un développement asymptotique des sommes partielles d’une série; pour la série harmonique:
![]()
qui est divergente et correspond à z(1), Euler trouve que :
![]()
est égal à ![]() , où en tend vers 0
pour n infini et g=0,5772156649... est une
constante connue sous le nom de constante d’Euler, dont on
ne sait toujours pas si elle est rationnelle ou irrationnelle. Au
chapitre XV de l’Introductio, Euler transforme la
série z(s), s entier, en un produit infini faisant
intervenir la suite des nombres premiers; la divergence de z(1)
lui donne alors non seulement l’infinitude des nombres
premiers, mais encore la divergence de la série des inverses des
nombres premiers, et même un équivalent lglgn pour la
somme des n premiers termes de cette série. Ailleurs, il
trouve une relation remarquable entre z(s) et la somme
qu’il attribuait formellement à la série divergente z(1-s)
[s entier£ 2]; cette équation fonctionnelle de la
fonction zêta devait être démontrée au XIXe siècle, pour s
complexe, par Malmsten, puis par Riemann qui en reconnut
l’importance et fonda sur elle l’étude de la
répartition des nombres premiers .
, où en tend vers 0
pour n infini et g=0,5772156649... est une
constante connue sous le nom de constante d’Euler, dont on
ne sait toujours pas si elle est rationnelle ou irrationnelle. Au
chapitre XV de l’Introductio, Euler transforme la
série z(s), s entier, en un produit infini faisant
intervenir la suite des nombres premiers; la divergence de z(1)
lui donne alors non seulement l’infinitude des nombres
premiers, mais encore la divergence de la série des inverses des
nombres premiers, et même un équivalent lglgn pour la
somme des n premiers termes de cette série. Ailleurs, il
trouve une relation remarquable entre z(s) et la somme
qu’il attribuait formellement à la série divergente z(1-s)
[s entier£ 2]; cette équation fonctionnelle de la
fonction zêta devait être démontrée au XIXe siècle, pour s
complexe, par Malmsten, puis par Riemann qui en reconnut
l’importance et fonda sur elle l’étude de la
répartition des nombres premiers .
Euler avait découvert encore d’autres relations entre les produits ou les séries infinies et la théorie des nombres, par exemple à propos du problème des partitions d’entiers en sommes d’entiers (Introductio, chap.XVI) et du produit:
![]()
qu’il avait su transformer en une série entière dont les exposants sont les nombres pentagonaux.
D’autres contributions importantes d’Euler concernent le calcul intégral, comme la résolution générale des équations différentielles linéaires à coefficients constants, la formule d’addition pour les intégrales elliptiques, la découverte des intégrales appelées maintenant eulériennes, dont l’une réalise l’interpolation de n! pour des valeurs non entières de n, l’étude de l’équation hypergéométrique et son intégration par une série entière, la résolution de nombreuses équations différentielles ou aux dérivées partielles par la méthode du facteur intégrant et les équations du calcul des variations. Comme d’Alembert l’avait reconnu à propos des cordes vibrantes en 1747, l’intégration d’une équation aux dérivées partielles fait intervenir des fonctions "arbitraires" (et non plus seulement des constantes arbitraires, comme pour les équations différentielles ordinaires); l’origine physique du problème conduisit Euler à prendre pour ces fonctions arbitraires des fonctions plus générales que celles de l’Introductio, définies par un graphe quelconque tracé à main libre, et non plus nécessairement par des expressions analytiques. Il s’ensuivit une controverse entre d’Alembert, Euler et D.Bernoulli, qui posa le problème du développement d’une fonction arbitraire en série trigonométrique; une partie importante des recherches du XIXe siècle a tourné autour de ces questions.
À son époque, Euler était à peu près le
seul à s’intéresser à la théorie des nombres. Tout au
long de sa carrière, il a essayé de prouver les résultats
laissés par Fermat sans démonstration: c’est ainsi
qu’il démontra le petit théorème de Fermat, selon lequel ap-1-1
est divisible par p si p est un nombre premier et
si a n’est pas divisible par p, et qu’il
en trouva une généralisation. Pour le "dernier" théorème de
Fermat, sur l’impossibilité de l’équation xn+yn=zn
pour n³ 3, Euler donna une démonstration dans le cas de n=3,
en admettant pour les nombres complexes de la forme ![]() , avec a
et b entiers, des propriétés arithmétiques analogues à
celles des entiers ordinaires; cela préfigure la théorie des
entiers algébriques qui devait être développée au XIXe
siècle par Kummer, Kronecker et Dedekind. On n’a toujours
pas de démonstration valable du théorème pour n
quelconque. Euler trouva une démonstration du fait que tout
nombre premier de la forme 4n+1 est somme de 2 carrés,
mais laissa à Lagrange la gloire de démontrer que tout entier
est somme de 4 carrés. Son habileté au calcul lui permit de
trouver que 225+1 est divisible par 641, alors que
Fermat avait conjecturé que 22n+1 est toujours
premier (c’est vrai pour 0£ n£ 4, mais on ne
connaît pas d’autre valeur de n pour laquelle ce
serait encore vrai); il découvrit une soixantaine de paires de
nombres amiables et démontra que les nombres parfaits pairs sont
tous de la forme déjà connue d’Euclide: 2n-1(2n-1),
avec 2n-1 premier (on ne sait toujours pas
s’il existe des nombres parfaits impairs).
, avec a
et b entiers, des propriétés arithmétiques analogues à
celles des entiers ordinaires; cela préfigure la théorie des
entiers algébriques qui devait être développée au XIXe
siècle par Kummer, Kronecker et Dedekind. On n’a toujours
pas de démonstration valable du théorème pour n
quelconque. Euler trouva une démonstration du fait que tout
nombre premier de la forme 4n+1 est somme de 2 carrés,
mais laissa à Lagrange la gloire de démontrer que tout entier
est somme de 4 carrés. Son habileté au calcul lui permit de
trouver que 225+1 est divisible par 641, alors que
Fermat avait conjecturé que 22n+1 est toujours
premier (c’est vrai pour 0£ n£ 4, mais on ne
connaît pas d’autre valeur de n pour laquelle ce
serait encore vrai); il découvrit une soixantaine de paires de
nombres amiables et démontra que les nombres parfaits pairs sont
tous de la forme déjà connue d’Euclide: 2n-1(2n-1),
avec 2n-1 premier (on ne sait toujours pas
s’il existe des nombres parfaits impairs).
Euler s’était aussi posé des problèmes relevant de ce que l’on appelle maintenant la topologie: le problème des ponts de Königsberg et la relation (connue sous le nom de formule d’Euler) entre les nombres de sommets, d’arêtes et de faces d’un polyèdre convexe.
À côté de ses ouvrages de recherche, Euler publia aussi des livres d’enseignement assez élémentaires, comme sa célèbre Algèbre (publiée en russe en 1768); la traduction française a été complétée par des notes de Lagrange sur la théorie des nombres.
Mécanique, physique, astronomie
Euler a publié de nombreux ouvrages relatifs à la technique. En 1736, paraît son traité de mécanique, Mechanica sive motus scientia analytice exposita, où, pour la première fois, la mécanique du point matériel est conçue et exposée comme une science rationnelle. En 1760, il donnera sa Theoria motus corporum solidorum seu rigidorum, où il définit le centre d’inertie, les moments d’inertie et les axes principaux d’inertie, tandis qu’il intègre les équations du mouvement d’un solide de révolution autour d’un point fixe de l’axe; son fils publiera, en 1790, une édition revue et augmentée de cet ouvrage.
Son traité de 1744, Methodus inveniendi lineas curvas maximi minimive proprietate gaudens, fonde le calcul des variations, dans la lignée des travaux de Jacques et Jean Bernoulli (l’ouvrage aura sur Lagrange une influence considérable). Un important appendice sur la détermination, par ce type de calcul, du mouvement d’un projectile dans un milieu résistant lui permet de justifier a posteriori le principe de la moindre action, de son ami P.-L.Maupertuis. Citons enfin, dans le domaine de la mécanique, ses études sur les cordes vibrantes; les discussions qui s’élevèrent entre D.Bernoulli, d’Alembert, Lagrange et lui-même le conduisirent à préciser la notion générale de fonction, sous une forme voisine de celle que l’on adopte maintenant: fonctions "arbitraires" données expérimentalement par un ou plusieurs arcs de courbes.
En hydrostatique, il généralise, en 1755, le principe de A.Clairaut et, la même année, il établit les équations générales de l’hydrodynamique.
Ses travaux d’astronomie se rattachent pour la plupart à la mécanique. L’étude des perturbations mutuelles de Jupiter et de Saturne fut proposée comme sujet de prix par l’Académie des sciences de Paris en 1748 et 1752. Il remporta les deux prix. Sur le mouvement parabolique des planètes, il publia, dès 1744, la formule dite de Lambert liant pour deux positions de l’astre, l’intervalle de temps, la corde et les deux rayons vecteurs.
Dans un travail de 1749 sur la précession des équinoxes, partant d’équations plus simples que celles de d’Alembert, il présente les résultats avec plus d’élégance. En 1753, dans sa théorie du mouvement de la Lune, qu’il améliore en 1772, il cherche à établir toutes les inégalités, remportant à ce sujet les prix de l’Académie des sciences de Paris pour 1770 et 1772.
En optique, Euler, à peu près seul parmi ses contemporains, soutenait une théorie ondulatoire de la lumière, comme on peut le voir dans ses Lettres à une princesse d’Allemagne. Pour lui, revenant aux conceptions de C.Huygens, "la lumière n’est autre chose qu’une agitation ou ébranlement causé par les particules de l’éther", "chaque couleur simple étant attachée à un certain nombre de vibrations qui s’achèvent dans un certain temps".
(CD Encyclopædia Universalis France, 1995)
![]()
Mis à jour le: 11/02/04
![]()