Menu:

Phare de l'île d'Aix
522- Equilibre d'un système matériel soumis à des forces concourantes
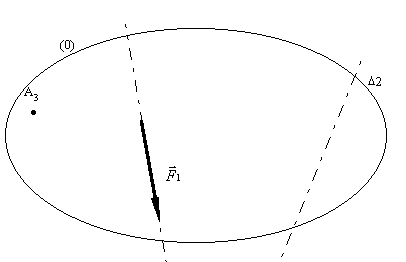
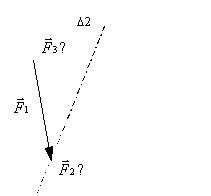
Soit un système matériel en équilibre soumis à trois forces concourantes $F↖{→}_1$ , $F↖{→}_2$ et $F↖{→}_3$. Les inconnues sont l’intensité de $F↖{→}_2$, l’intensité et la direction de $F↖{→}_3$. On connaît $A3$, le point d’application de $F↖{→}_2$.
Le système étant en équilibre, les équations suivantes sont vérifiées en tous points O de l'espace:
- $F↖{→}_{1} +F↖{→}_{2} +F↖{→}_{3}=0↖{→}$
- $ M↖{→}_{F↖{→}_1}(O) +M↖{→}_{F↖{→}_2}(O) +M↖{→}_{F↖{→}_3}(O)= 0↖{→}$
De même que dans les paragraphes précédents, on doit tracer un dynamique et un funiculaire.
Tracé du dynamique:
Le dynamique vérifie l'équation: $F↖{→}_{1} +F↖{→}_{2} +F↖{→}_{3}=0↖{→}$
Pour tracer le dynamique, il suffit de tracer la force $F↖{→}_1$. On devrait tracer la force $F↖{→}_2$ au bout de $F↖{→}_1$, puis $F↖{→}_3$ au bout de $F↖{→}_2$. Le système étant à l'équilibre, la résultante des trois forces est nulle et donc l'extrémité de $F↖{→}_3$ correspond à l'origine de $F↖{→}_1$. Le dynamique est fermé.