EXERCICE 5-1:
|
Soit une plaque demi-circulaire de rayon R. L'axe Ox coupe la plaque en deux morceaux identiques a)- Déterminer la position de son centre de gravité G b)- Déterminer sa matrice d'inertie au point O c)- En déduire sa matrice d'inertie au point G |
|
EXERCICE 5-2:
|
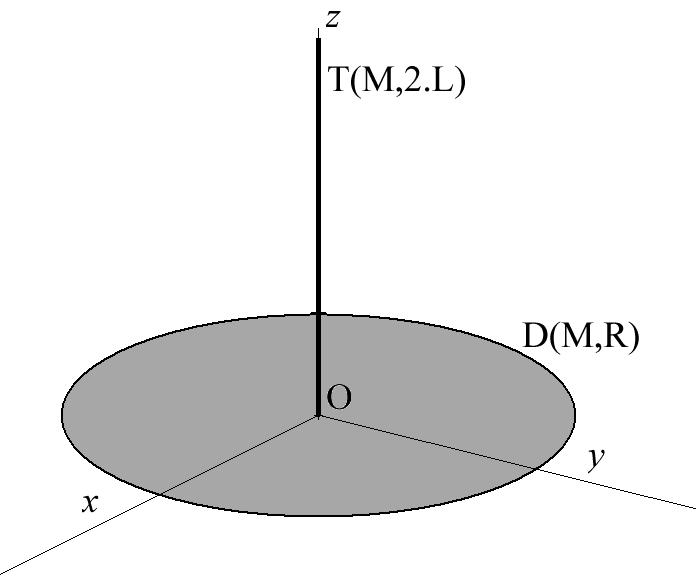
Soit un solide constitué d'un disque (D) de masse M et de rayon R et d'une tige (T) de même masse M de longueur 2L soudée au centre O du disque (D). a)- Déterminer la matrice d'inertie du solide(S) au point O b)- En déduire sa matrice d'inertie à l'autre extrémité A de la tige (T) |
 |
EXERCICE 5-3:
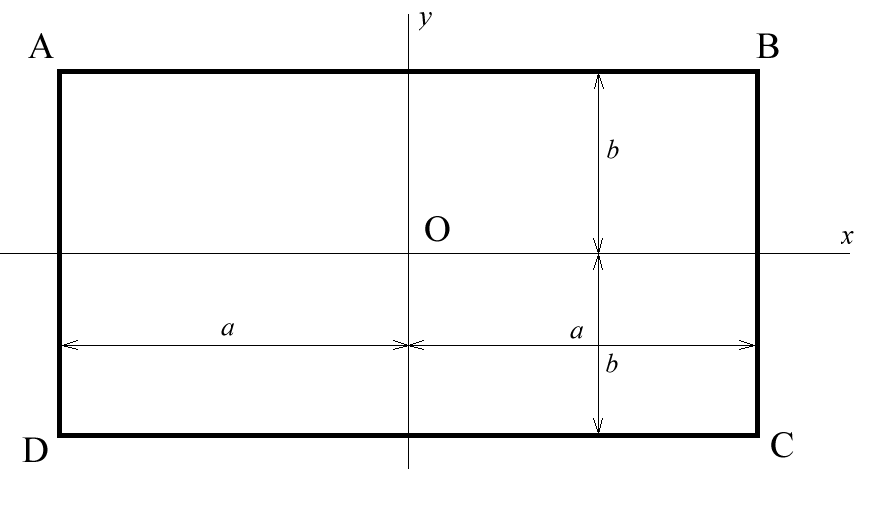
Un cadre rectangulaire (S) est constitué de quatre tiges rectilignes homogènes:
AB et CD de masse linéique r et de longueur 2.a
AD et BC de même masse linéique de longueur 2.b
a)- Déterminer la matrice d'inertie du cadre (S) en son centre O
On ajoute une masse ponctuelle m au point B
b)- Calculer la nouvelle matrice du cadre (S) chargé en B exprimée au point O
c)- Calculer le moment d'inertie du cadre par rapport à la droite D0B
EXERCICE 5-4:
|
Soit une plaque de forme triangle rectangle de base b et de hauteur h.
1) En utilisant le théorème de GULDIN, déterminez les coordonnées de G, centre de gravité de la plaque. 2)- Déterminer sa matrice d'inertie en O 3)- En déduire sa matrice d'inertie en G |
|
Mis à jour le: 11/02/04
