Le torseur dynamique en un point A se définit par la donnée de deux vecteurs:
· La résultante dynamique:  · Le moment dynamique au point A: |
112- Corps matériels homogènes
De même, pour les corps matériels homogènes, on aura:
· La résultante dynamique:  · Le moment dynamique au point A: |
| Remarque: · L’accélération dépend du repère de référence choisi et donc le torseur dynamique dépend également du repère de référence choisi. |
12-
Expression du torseur dynamique d’un système
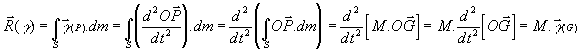
d’où:
 |
a-
Relation entre 
et 
· 
· 
Calculons la dérivée du moment cinétique en A:
· 
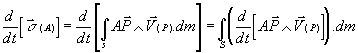car 
et 
sont indépendants
dérivation d'un produit
or
soit,
étant indépendant de
d’où:
· Attention à ne pas confondre cette relation avec une relation de transport d'un moment de torseur.
Remarques: On peut
écrire  lorsque:· A est un point fixe · G est un point fixe · A est confondu avec G · |
b- Formule de transport
Le torseur dynamique obéit aux mêmes règles que les autres torseurs et donc:
 |
quelques soient les points A et B.
2-
PRINCIPE FONDAMENTAL DE LA DYNAMIQUE
Le principe
fondamental de la dynamique (PFD) indique qu’à
chaque instant, le torseur des actions extérieures
s’appliquant à un système est équivalent au
torseur dynamique de ce système. C’est à dire, en
un point quelconque A, nous avons:
|
22- Exemple: Disque roulant sur un plan
incliné
221 Calcul du torseur dynamique du disque D
· 
· 
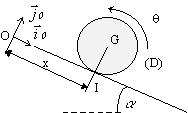
d’où on en déduit: 
· 
or 
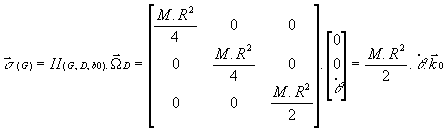
d’où:
Soit l’expression du torseur dynamique de D:
·  · |
222- Bilan des actions extérieures sur le
solide
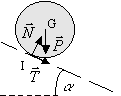
· Pesanteur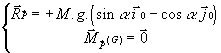
· Action de contact avec le sol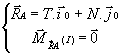
Soit en définitive:
·  · |
223 Principe Fondamental de la dynamique
En appliquant le principe fondamental de la dynamique au point G:
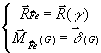on obtient: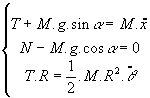 
Ou encore: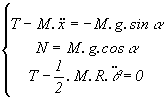 
Nous sommes en présence d’un
système de trois équations à quatre inconnues
. Pour le
résoudre, il nous faut une équation supplémentaire que
l’on va obtenir en examinant les conditions de roulement
au point de contact I entre le disque et le plan incliné.
224 Hypothèse de roulement sans glissement
a- Equation supplémentaire
Si on fait l’hypothèse qu’il y a roulement sans glissement du disque (D) sur le plan (P), alors la vitesse de glissement de (D) sur (P) est nulle. Soit:
· 
le plan étant fixe
· 
La condition de roulement sans glissement nous fournit l’équation:
soit en dérivant par rapport au temps:
on résoud alors le système: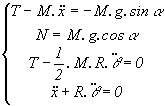 
on obtient après résolution:
 |
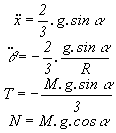b- Vérification à effectuer
Il faut cependant vérifier:
· 
traduisant l’existence du contact en I
soit 
et donc
 |
· 
soit 
et donc
 |
Dans le cas où il y a roulement avec glissement on a l'équation:
soit en définitive 
Il faut
étudier les deux cas posssibles.
a-
Première équation supplémentaire possible: 
Supposons dans un premier temps
que
Il faut alors résoudre le système:
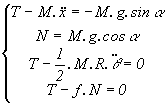
soit après résolution:
 |
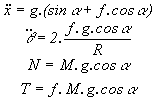b- Vérifications à effectuer
il est cependant nécessaire de vérifier les conditions suivantes:
· 
traduction de l’existence du contact en I
soit 
et donc
 |
· 
ce qui est immédiat puisque 
et 
sont
portés par le même vecteur 
· 
soit 
soit après simplification:
 |
ce qui est
impossible car 
est strictement positif
L'équation supplémentaire 
nous amène
donc à une impossibilité physique; c'est par conséquent
l'autre équation qui est correcte.
c-
Autre équation possible: 
Il faut dans ce cas résoudre le système:
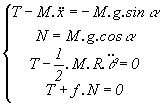
on obtient:
 |
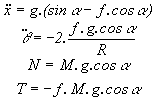d- Vérifications à effectuer
il faut toujours vérifier les conditions suivantes:
· soit et donc
|
· ce qui immédiat puisque et sont tous
deux portés par le vecteur
· soit 
soit après simplification:
 |
Nous pouvons remarquer que cette condition est complémentaire de celle trouvée dans l'hypothèse du roulement sans glissement.
En définitive la
solution de ce problème varie suivant les valeurs
respectives de  et 
si si |
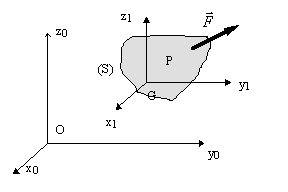
Soit un point se déplaçant sur
sa trajectoire (s). Appelons 
la vitesse du point P, tangente à la
trajectoire et 
une force appliquée en P.
La puissance instantanée
correspondant à s’écrit:
 |
La puissance étant également définie comme un travail par unité de temps, on en déduit:
d’où la définition du travail:
 |
| Remarque: · Puissance et travail sont des SCALAIRES |
312 Travail d’une force appliquée en
un point quelconque d'un solide (S)
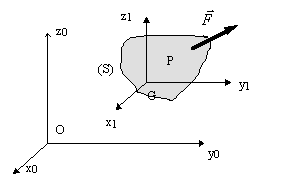
On a 
or 
d’où: 
soit d’après les propriétés des produits mixtes:
or 
d’où:
 |
Le premier terme représente le travail de translation et le second le travail de rotation autour de G.
a-Translation pure:
et donc 
Si de plus 
est
indépendant du temps:
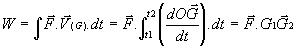avec G1 et G2 représentant
respectivement les positions de G aux instant t1 et t2.
b-Rotation autour d’un point fixe O du système (S):
32-
Energie potentielle d’un système
Le calcul de l’expression du travail n’est pas toujours possible, en particulier lorsque le travail dépend de la trajectoire suivie pour passer d’un état initial à un état final, ou dans le cas du glissement.
Lorsque le travail dépend
uniquement des positions initiales et finales, on dit que les
forces correspondantes dérivent d’un potentiel
et que le travail 
est égal à l’opposée de la variation de l’énergie
potentielle 
:
 |
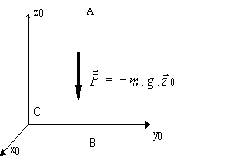
a- Pesanteur
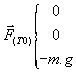et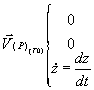 
 |
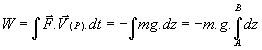
b- Ressort
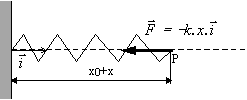
Pour un ressort linéaire de raideur k:
et 
 |
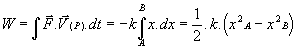
De même pour un ressort de torsion de constante c, on obtient:
 |
33- Principe de conservation de
l’énergie
| Hypothèse: Les forces extérieures agissant sur le système dérivent d’un potentiel; c’est à dire que l’énergie potentielle peut être calculée. |
Soit un solide (S) soumis
uniquement à une force 
au point P. Le travail élémentaire 
peut
s’écrire:
D’après le principe fondamental de la dynamique:
· 
· 
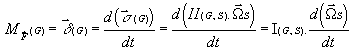
on introduit ces expressions dans
l’ecriture de 
, on obtient:
or 
Le premier terme 
représente 
de
translation et le second terme 
représente
de
rotation.
d’où:
On en déduit le principe de conservation de l'énergie (mécanique):
 |
Reprenons l’exemple du disque
qui roule sur un plan incliné avec l’hypothèse du
roulement sans glissement; soit: 
Dans ce cas, les hypothèses du théorème de conservation de l’énergie sont vérifiées. On peut montrer que le travail des forces de contact est nul.
· 
· 
En utilisant 
, on
obtient:
En dérivant par rapport au temps, on obtient:
soit si 
:
 |
| Remarques: · Dans le cas du roulement avec glissement, le travail des forces de frottement est inconnu, on ne peut donc pas calculer l’énergie potentielle. Le principe de conservation de l’énergie (mécanique) ne s’applique pas. · Le principe de conservation de l’énergie mécanique découle du principe fondamental de la dynamique et donc, il n’apporte pas une nouvelle équation supplémentaire. Par contre il permet d’obtenir directement une équation régissant le mouvement du système étudié, sans s’occuper des efforts appliqués au systême. |
Mis à jour le: 11/02/04
1- TORSEUR DYNAMIQUE 
11- Définitions 
et 
sont équipollents
alors 
