Soit une distribution de masses
ponctuelles
(en un point 
se trouve concentrée la masse 
); le
torseur cinétique en un point A se définit par la donnée de
deux vecteurs:
· La résultante cinétique:  · Le moment cinétique au point A: |
112- Corps matériels homogènes
De même, pour un corps matériel homogène, on aura:
· La résultante cinétique:  · Le moment cinétique au point A: |
| Remarque: · La vitesse d'un point ou d'un solide dépend du repère de référence choisi et donc le torseur cinétique dépend également du repère de référence choisi. |
12-
Expression du torseur cinétique d’un système
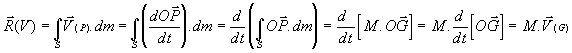
d’où:
 |
a- Formule de transport
Le torseur cinétique obéit aux mêmes règles que les autres torseurs et donc:
 |
quelques soient les points A et B.
b- Moments cinétiques de translation et de rotation
Soient:
(T0) un repère fixe 
de
référence
(Ts) un repère mobile 
lié au
solide (S) (G représente le centre de gravité de (S).)
Dans ce cas, on peut écrire d'après la formule de transport des vitesses de deux points d'un même solide:
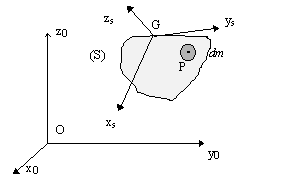
représentant le vecteur rotation du
solide (S) dans son mouvement par rapport à (T0)
On peut écrire:
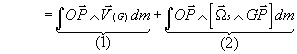
· Calcul du premier terme: en tenant compte de l'indépendance de G vis à vis du choix de l'élément d'intégration dm et de la définition du centre de gravité
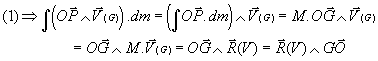
· Calcul du second terme:
On peut écrire: 
· 
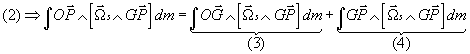
car 
et 
sont
indépendant de 
· 
soient: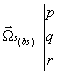 
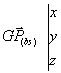On a alors:
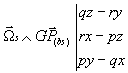
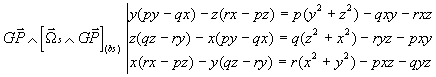
d'ou:
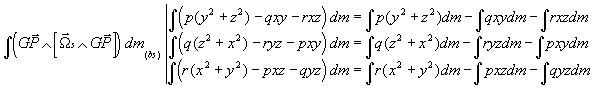
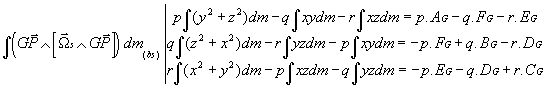
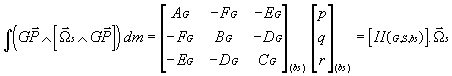
D'ou en définitive:
 |
en identifiant par rapport à la formule de transport du moment cinétique:
on en déduit:
 |
· 
correspond au moment cinétique qu'on
obtiendrait si G était fixe. On peut aussi dire que c'est le
moment cinétique du à la rotation autour du point G: c'est le moment
cinétique de rotation.
· 
correspond au moment cinétique du solide,
en concentrant toute sa masse au centre d'inertie G, se
déplaçant comme un point matériel par une translation
rectiligne ou circulaire: c'est le moment cinétique de
translation.
| Remarques: · Si on a un mouvement autour d'un point fixe
O, la vitesse d'un point P quelconque du solide (S) peut
s'écrire:. · Si, de plus, on a un mouvement plan autour
de Oz par exemple,
|
L'énergie cinétique d'un système de solides ponctuels s'exprime par:
 |
212- Corps matériels homogènes
De même, pour les corps matériels homogènes, on aura:
 |
| Remarques: · · L'énergie cinétique est un SCALAIRE, unité (W.s). |
22-
Energies cinétique de translation et de rotation
Soient:
(T0) un repère fixe
(Ts) un repére mobile lié au
solide (S) (G représente le centre de gravité de (S).)
Dans ce cas, on peut écrire d'après la formule de transport des vitesses de deux points d'un même solide:
· 
, d'où:
d'après la propriété des
produits mixtes: 
, on obtient:
En utilisant les propriétés
d'associativité vectorielle et l'invariance de
et 
par rapport
à l'élément d'intégration 
, on peut écrire:
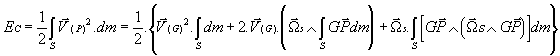
On a de plus:
· 
· 
par définition du centre de gravité G du solide
(S)
· 
suivant le calcul du terme (4) effectué au
paragraphe 122-b
D'où, en définitive:
 |
· 
correspond à l'énergie cinétique du solide en
concentrant toute sa masse au centre d'inertie G, se déplaçant
comme un point matériel par une translation rectiligne ou
circulaire: c'est l'énergie cinétique de translation.
· 
correspond à l'énergie cinétique qu'on
obtiendrait si G était fixe. On peut aussi dire que c'est
l'énergie cinétique du à la rotation autour du point G: c'est l'énergie
cinétique de rotation.
| Remarques: · Si on a un mouvement autour d'un point fixe
O on obtient: · Si on a un mouvement de rotation autour d'un axe fixe passant par O; Oz par exemple:
|
Mis à jour le: 11/02/04
d'où on obtient: 
est tel que p=0, q=0. On obtient
alors:
avec
vitesse
de rotation autour de l'axe Oz
est un scalaire
avec
vitesse
de rotation autour de l'axe Oz (
)