La géométrie des masses permet de déterminer les centres de gravité et la matrice d'inertie d'un solide, notions utilisées dans les chapitres suivants
Chap. 5: GEOMETRIE DES MASSES
![]()
11-
Systèmes de solides ponctuels
![]()
![]()
![]()
![]()
· Soit une distribution de masse (Pi, mi), le centre de gravité G est défini par le barycentre des n points Pi affectés des coefficients égaux aux masses mi.
|
ou
· Ligne matérielle: (tige, fil, ...)
|
Pour une tige homogène, on a:
|
Exemple: demi-cerceau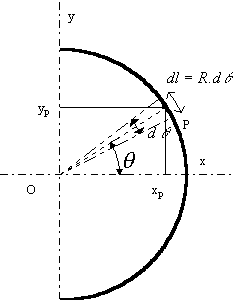
![]()
![]()
![]()
![]()
d’où:
 |
· Surface matérielle: (plaque, coque, ...)
Pour une surface homogène, on a:
· Volume matériel:
Pour un volume homogène, on a:
![]()
122- Simplifications éventuelles
![]()
![]()
![]()
![]()
![]()
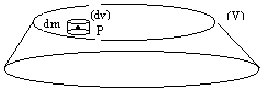
· Si un ensemble de masse M est composé de plusieurs solides de masse Mi, il est possible de trouver le centre de gravité G en concentrant les masses Mi aux centres de gravité Gi et en écrivant:
![]()
· Si un corps admet un plan, un axe ou un centre de symétrie, alors son centre de gravité se trouve dans ce plan, sur cet axe ou ce point.
a) Théorèmes de GULDIN
![]()
![]()
![]()
![]()
![]()
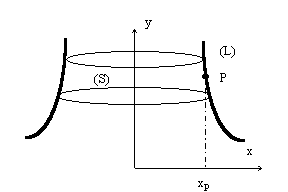
· Soit une courbe (L) tournant autour de l'axe Oy , ne le coupant pas. L'élément dl engendre une surface ds telle que:
![]()
La surface totale engendrée sera :
![]()
compte tenu de la définition du centre de gravité d'une ligne matérielle.
· Soit une surface plane (S) tournant autour de l'axe Oy , ne le coupant pas. L'élément ds engendre un volume dv tel que:
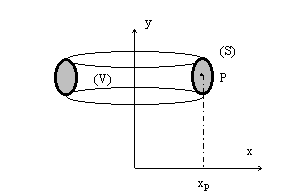
![]()
Le volume total engendré sera :
![]()
compte tenu de la définition du centre de gravité d'une surface matérielle
· Exemple: Centre de gravité d'une demi plaque circulaire.
![]()
![]()
· Surfaces planes définies sous forme cartésienne
|
On connaît P est le centre de gravité de
|
|
d'où: 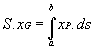 et
et 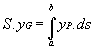
· Surfaces planes définies sous forme polaire
|
|
On connaît la fonction donnant la
limite de la surface l'élément P est le centre de gravité de |
|
· Surfaces de révolution Si Oz est l'axe de révolution, on
a: L'élément de surface
car Volumes de révolution De même, on aura:
|
|
| Remarque: · Il est nécessaire de transformer toutes les quantités en fonction de variables indépendantes avant de procéder à l'intégration. |
2-
MOMENTS D'INERTIE ET PRODUITS D'INERTIE
![]()
![]()
![]()
· Le moment d'inertie d'un système (Pi, mi) par rapport à un plan p , à une droite D ou à un point O est défini par:
![]() représentant la distance de
représentant la distance de ![]() au plan p , à
la droite D ou au point O
au plan p , à
la droite D ou au point O
| Remarque: · Un moment d'inertie est toujours positif ou nul.
|
· On appelle produits d'inertie d'un système (Pi, mi) par rapport à un système d'axe Ox, Oy, Oz les expressions:
 |
· Le moment d'inertie d'un corps matériel homogène (S) par rapport à un plan p , à une droite D ou à un point O est défini par:
![]() représentant la distance du point courant
représentant la distance du point courant
![]() ,
centre de gravité de l'élément élémentaire
,
centre de gravité de l'élément élémentaire ![]() , au plan p , à
la droite D ou au point O
, au plan p , à
la droite D ou au point O
· Les produits d'inertie se définissent alors par:
 |

· Expressions analytique des moments d'inertie
¨ par rapport au point O:

![]()
¨ par rapport aux axes Ox, Oy, Oz
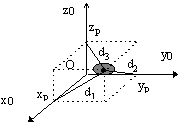 Axe Ox:
Axe Ox: ![]()
Axe Oy: ![]()
Axe Oz: ![]()
Soit:
¨ par rapport aux plans de bases yOz, xOy, xOz
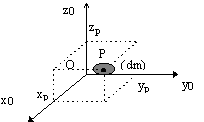
Plan yOz: ![]()
Plan xOz: ![]()
Plan xOy: ![]()
Soit:
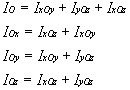 |
Pour un système d'axes Ox, Oy, Oz, on définit la matrice d'inertie d'un solide en un point O sous la forme:
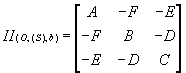 |
24-
Transport des moments et produits d'inertie
![]()
![]()
![]()
![]()
241- Axes parallèles aux axes de bases et
passant par G
![]()
![]()
![]()
![]()
![]()
2411- Moments d’inertie: Théorème de HUYGENS
![]()
![]()
![]()
![]()

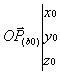


![]()
![]() or
or

· d’où: ![]()
![]()
car a et b sont des constantes
indépendantes de ![]() .
.
· G est le centre de gravité de (S) d’où 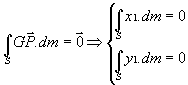
· de plus ![]() d’où:
d’où:
De même , on obtiendrait:
| et |
En généralisant, on obtient:
| Le moment d’inertie
d’un solide (S) par rapport à un axe D passant par un point quelconque 0 est égal
à la somme du moment d’inertie par rapport à un
axe parallèle à D passant par G le centre de
gravité de (S) et le produit de la masse M du solide par
le carre de la distance de l'axe à G:
|
![]()
![]() or
or

d’où: ![]()
![]()
car b et c sont des constantes
indépendantes de ![]() .
.
G est le centre de gravité de (S)
d’où 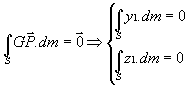
de plus ![]() d’où:
d’où:
De même , on obtiendrait:
| et |
 242-
Axes quelconque passant par O, sommet du trièdre de base
242-
Axes quelconque passant par O, sommet du trièdre de base
![]()
![]()
![]()
![]()
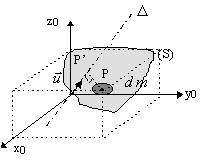
Soit (T0) Ox0y0z0
un trièdre de base et D un axe quelconque passant par 0 et de
vecteur directeur unitaire ![]() .
.
Soit P’ la projection orthogonale du point P sur l’axe D
P’P est la distance de P à l’axe D d’où:
![]()
![]() or
or 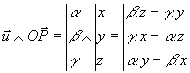
![]()
On obtient finalement:
Ou sous forme matricielle:
| Remarques: · On appelle axes principaux d’inertie, les axes pour lesquels les produits d’inertie sont nuls · Dans le cas des surfaces planes, deux des produits d’inertie sont nuls. ex surface dans le plan Oxy: pour tous points P de la surface, z = 0 d’où D = E = 0 · Dans le cas des solides de révolution, les axes perpendiculaires à l’axe de révolution jouent le même rôle. ex volume de
révolution autour de Oz: D’après les relations vues précédemment, on en déduit que A = B = C/2 |
Matrices en G |
Matrices en A |
Schémas |
| Tige | (M,L) | |
|
|
|
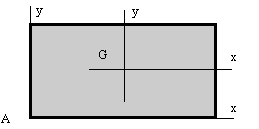
| Plaque rectangulaire | (M, 2a*2b) | |
|
|
 |
| Parallélépidéde rectangle | (M, 2a*2b*2c) | |
|
|
|
Matrices en G |
Matrices en A |
Schémas |
| Cylindre plein | (M,R,H) | |
|
|
|
| Couronne circulaire | (M, R) | |
|
|
|
| Plaque circulaire | (M, R) | |
|
|
|
| Sphère creuse | (M, R) | |
|
|
|
| Sphère pleine | (M, R) | |
|
|
![]()
Mis à jour le: 11/02/04
![]()