La cinématique est la partie de la mécanique qui étudie les mouvements des corps par rapport au temps, indépendamment de leurs causes.
Chap.4: CINEMATIQUE
![]()
1-
POSITIONNEMENT D'UN POINT OU D'UN SOLIDE
![]()
![]()
![]()
|
· Dans le plan: 2 paramètres coordonnées cartésiennes
coordonnées polaires
|
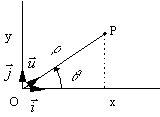
|
|
· Dans l'espace: 3 paramètres coordonnées cartésiennes
coordonnées cylindriques
coordonnées sphériques |
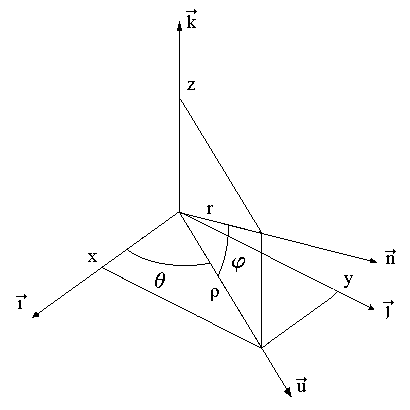
|
· Dans le plan: 3 paramètres, deux pour préciser la position d'un point particulier du solide et un paramètre de rotation

· Dans l'espace: 6 paramètres; trois
paramètres pour préciser la position d'un point particulier P
du solide (paramètres de translation et 3 parametres fixant la
position d'un point quelconque M par rapport à ce point P (en
général paramètres de rotation). Ces paramètres sont appelés
angles d'EULER: précession,
nutation, rotation propre.
· Dans le cas d'un solide ayant un point fixe, 3 paramètres suffisent.
2-
NOTIONS DE MOUVEMENT ET DE REPOS - REPERES ABSOLU ET RELATIF -
REPERES DE REFERENCES ET DE PROJECTION
![]()
![]()
![]()
![]()
Un point P est dit en mouvement par rapport à un repère si au moins une de ses coordonnées varie en fonction du temps. Si toutes ses coordonnées restent constantes, on dit qu'il est au repos par rapport à ce repère.
Cette notion est relative: un voyageur assis dans un train est en mouvement par rapport à un repère lié à la terre et est au repos par rapport à un repère lié au train.
Dans la suite de ce cours, nous appellerons (T0) le repère absolu ou de référence et (T1) le repère mobile. Les bases associées à ces repères seront toujours orthonormées directes.
On appelle mouvement d'entraînement le mouvement permettant de passer de (T0) à (T1).

Examinons maintenant la différence entre repère de référence et repère de projection.
Pour cela, considérons l'exemple d'un mouvement circulaire uniforme (w constante).
Dans ce cas, on sait que la
vitesse est tangente au cercle et que son module est R.w . Le
repère de référence est (T0) et R. w
représente la vitesse par rapport à ce repère. On peut
exprimer les composantes du vecteur vitesse dans (T0),
mais il est plus facile de les exprimer dans le repère mobile (T1),
en effet on a simplement ![]() .
.
On a alors exprimé la vitesse du point P par rapport à (T0) en exprimant ses composantes dans un autre repère (T1). (T0) est le repère de référence tandis que (T1) est le repère de projection.
21-
Mouvement d'entraînement de translation
![]()
![]()
![]()
![]()
(T1) se déduit de (T0)
par une translation de vecteur ![]() :
:
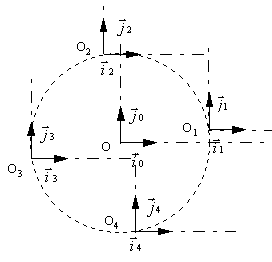
Le sommet du repère mobile (T1) se déplace sur un cercle, mais ses vecteurs restent équipollents à ceux de (T0) .

23-
Mouvement d'entraînement de rotation
![]()
![]()
![]()
![]()
Le sommet du repère mobile (T1) se déplace sur un cercle, et ses vecteurs suivent le mouvement de rotation .
On appelle trajectoire d'un point le lieu de ce point P dans un repère donné. La trajectoire dépend du repère choisi.
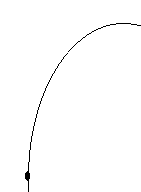
Exemple: trajectoire d'une goutte de pluie vue d'un repère mobile (véhicule en mouvement)
312- Vitesses et accélérations d'un point:
![]()
![]()
![]()
![]()
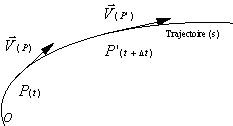
· Vitesse moyenne de P à P':
· Vitesse instantanée de P:
Si ![]() alors
alors ![]() avec
avec ![]() le vecteur
unitaire tangent à la trajectoire (S)
le vecteur
unitaire tangent à la trajectoire (S)
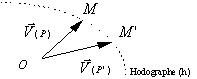
Construisons l'hodographe,
lieu des points M et M' tels que ![]() , O étant un
point fixe
, O étant un
point fixe
· Accélération moyenne de P à P':
· Accélération instantanée de P:
32-
Expressions analytiques de la vitesse et de l'accélération d'un
point
![]()
![]()
![]()
![]()
![]()
· ![]()
· ![]()
![]()
·
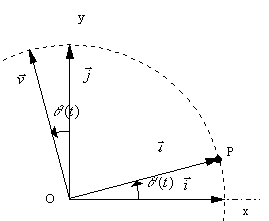
322- Application à la dérivation d'un
vecteur mobile
![]()
![]()
![]()
![]()
![]()
Soit le point P tel que ![]() avec
avec ![]()
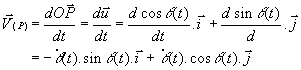

soit:
| Remarques: ·
En identifiant, on en
déduit: · Ce vecteur est appelé vecteur rotation et est tel que: - son axe est perpendiculaire au plan où se produit la rotation - son module est égal à
la vitesse angulaire · De la même façon, on obtient: |
· ![]()
· 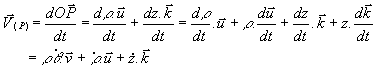
![]()
· ![]()
![]()
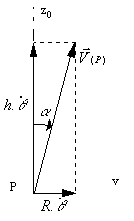
· Cas particulier du mouvement hélicoïdal
¨
![]() d'où on en déduit
d'où on en déduit ![]()
¨ ![]() , h étant le pas de l'hélice.
, h étant le pas de l'hélice.
![]()
![]()
![]() , le vecteur vitesse forme un angle
constant avec la génératrice du cylindre sur lequel
s’enroule l’hélice.
, le vecteur vitesse forme un angle
constant avec la génératrice du cylindre sur lequel
s’enroule l’hélice.
Si ![]() , le
mouvement est dit hélicoïdal uniforme
, le
mouvement est dit hélicoïdal uniforme
· Cas particulier du mouvement plan
¨ ![]() d'où on en déduit
d'où on en déduit ![]()


· Cas particulier du mouvement circulaire
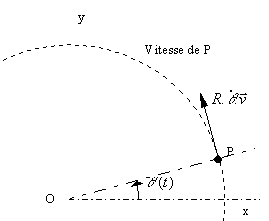
¨ ![]() d'où on en déduit
d'où on en déduit ![]()
¨ ![]() d'où on en déduit
d'où on en déduit ![]()

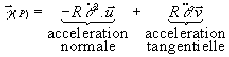

Si ![]() avec w
constante, le mouvement est dit circulaire uniforme
avec w
constante, le mouvement est dit circulaire uniforme

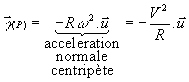
33- Dissociation des paramètres
Supposons que la position du point
P dépende de n paramètres indépendants. Il est possible de
bloquer tous les paramètres sauf un, q i
que l'on fait varier en fonction du temps. On obtient alors la
vitesse ![]() relative
au paramètre q i. En additionnant toutes ces
vitesses, on détermine la vitesse du point P.
relative
au paramètre q i. En additionnant toutes ces
vitesses, on détermine la vitesse du point P.
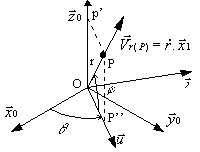
Exemple d'un point P dont la
position est exprimée en coordonnées sphériques: ![]() :
:
![]()
· ![]() varie,
varie, ![]() sont bloqués
sont bloqués
Le mouvement de P est une
translation le long de l'axe ![]() . La vitesse de déplacement du point P
est donc:
. La vitesse de déplacement du point P
est donc: ![]()
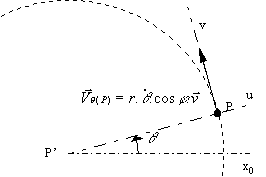
· ![]() varie,
varie, ![]() sont bloqués
sont bloqués
Le mouvement du point P est une
rotation de centre P' de rayon ![]() et de vitesse angulaire
et de vitesse angulaire ![]() , dans le
plan
, dans le
plan ![]() .
La vitesse de P est donc:
.
La vitesse de P est donc: ![]()

· ![]() varie,
varie, ![]() sont bloqués
sont bloqués
Le mouvement du point P est une
rotation de centre O de rayon ![]() et de vitesse angulaire
et de vitesse angulaire ![]() dans le plan
dans le plan
![]() . La
vitesse de P est donc:
. La
vitesse de P est donc: ![]()
· globalement la vitesse du point P par rapport à (T0) sera donc:
![]()
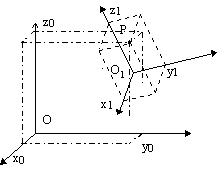
Soit deux repères:
· T0![]() le repère de référence fixe
le repère de référence fixe
· T1![]() le repère mobile
le repère mobile
Appelons ![]() les
coordonnées d'un point P dans (T1); la relation
vectorielle
les
coordonnées d'un point P dans (T1); la relation
vectorielle
![]() peut s'écrire
peut s'écrire![]()
En dérivant l'expression du
vecteur ![]() ,
nous obtenons:
,
nous obtenons:
![]() soit:
soit:
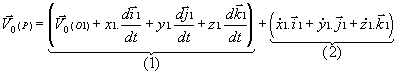
· Le terme (1) représente la vitesse qu'aurait le
point P si ses coordonnées ![]() dans (T1) étaient constantes,
c'est à dire si P était fixe par rapport à (T1). Ce
terme représente la vitesse d'entraînement du point P .
On la note:
dans (T1) étaient constantes,
c'est à dire si P était fixe par rapport à (T1). Ce
terme représente la vitesse d'entraînement du point P .
On la note:![]() .
.
· Le terme (2) représente la vitesse qu'aurait le
point P si les paramètres fixant la position de (T1)
par rapport à (T0) étaient constants, c'est à dire
si (T1) était fixe par rapport à (T0).
C'est la vitesse du point P par rapport à (T1)
appelée aussi la vitesse relative du point P . On la
note:![]() .
.
Ainsi on obtient la vitesse absolu du point P ou vitesse du point P par rapport à (T0) par
42- Cas où P est fixe dans (T1):
Transport de vitesses
![]()
![]()
![]()
![]()
Si le point P est fixe par rapport au repère (T1), c'est à dire si le repère (T1)est lié au mouvement du solide auquel appartient le point P, alors la vitesse relative de P est nulle, d'où on peut écrire:
![]()
Or nous pouvons écrire:
![]() est ici le vecteur rotation permettant de
passer du repère de référence (T0) au repère
mobile (T1); on le note également
est ici le vecteur rotation permettant de
passer du repère de référence (T0) au repère
mobile (T1); on le note également ![]() . D'où:
. D'où:

soit:
| Remarques: · Le point O1 est l'origine du repère (T1).
Le repère (T1) est lié au solide (S) auquel
appartient le point P, on peut donc noter
· Cette relation est appelé relation de transport des vitesses, valable entre deux points appartenant à un même solide, et semblable dans sa forme à une relation de transport d'un moment de torseur. |
En dérivant l'expression du
vecteur ![]() ,
nous obtenons l'accélération:
,
nous obtenons l'accélération:
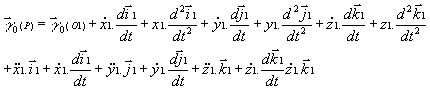
soit:
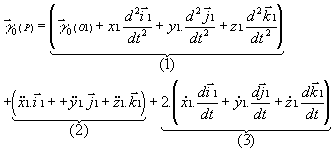
· Le terme (1) représente l'accélération qu'aurait
le point P si ses coordonnées ![]() dans (T1) étaient constantes,
c'est à dire si P était fixe par rapport à (T1). Ce
terme représente l'accélération d'entraînement du
point P . On la note:
dans (T1) étaient constantes,
c'est à dire si P était fixe par rapport à (T1). Ce
terme représente l'accélération d'entraînement du
point P . On la note:![]() .
.
· Le terme (2) représente l'accélération qu'aurait
le point P si les paramètres fixant la position de (T1)
par rapport à (T0) étaient constants, c'est à dire
si (T1) était fixe par rapport à (T0).
C'est l'accélération du point P par rapport à (T1)
appelée aussi l'accélération relative du point P . On
la note:![]() .
.
· Le terme (3) est appelée l'accélération
de CORIOLIS et notée:![]() .
.
Ainsi on obtient l'accélération absolu du point P ou accélération du point P par rapport à (T0) par
431- Expression vectorielle de
l'accélération de CORIOLIS
![]()
![]()
![]()
![]()

Or nous pouvons écrire:
![]() est le vecteur rotation permettant de
passer du repère de référence (T0) au repère
mobile (T1), on peut dire que c'est le vecteur
rotation d'entrainement, noté
est le vecteur rotation permettant de
passer du repère de référence (T0) au repère
mobile (T1), on peut dire que c'est le vecteur
rotation d'entrainement, noté ![]()
![]()
soit:
432- Cas où l'accélération de CORIOLIS est
nulle
![]()
![]()
![]()
![]()
L'accélération de CORIOLIS est
nulle si le produit ![]() est nul, ce qui se produit pour:
est nul, ce qui se produit pour:
· ![]() : Le mouvement d'entraînement est une translation
: Le mouvement d'entraînement est une translation
· ![]() : Le point P est fixe dans le repère (T1)
: Le point P est fixe dans le repère (T1)
· ![]() et
et ![]() sont colinéaires: cas très rare
sont colinéaires: cas très rare
44-
Vitesse de glissement - Condition de roulement sans glissement
![]()
![]()
![]()
Considérons deux solides (S1) et (S2) en contact à un instant donné.
Appelons I1 et I2
les points de (S1) et (S2) en contact à
cet instant. On définit la vitesse de glissement ![]() du solide (S1)
par rapport le solide (S2) par:
du solide (S1)
par rapport le solide (S2) par:
Si la condition de roulement sans glissement est réalisée, cette vitesse est nulle soit:
![]()
| Remarques: · Les points I1 et I2 ne coïncident qu'à un instant t, aussi l'égalité de leurs vitesses ne conduit en aucun cas à l'égalité de leurs accélérations:
· Les points I1 et I2 ne sont pas fixe par rapport à (S1) et (S2) |
![]()
Mis à jour le: 11/02/04
![]()