23- Actions mécaniques exercées sur des liaisons
usuelles parfaites
422- Solides soumis à trois forces extérieures
non parallèles
423- Solides soumis à l'action d'au moins
quatre forces extérieures
51- Détermination graphique de la résultante d'un
système de forces.
521- Equilibre d'un système matériel soumis à
des forces parallèles
522- Equilibre d'un système matériel soumis à
des forces concourantes
(N.m-1).
située au centre de la ligne de contact  |
 |
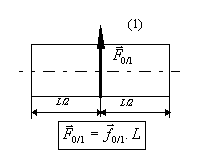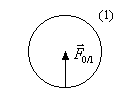
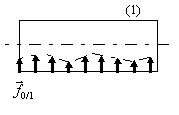
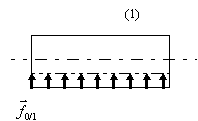
ex: Boite sur un plan.
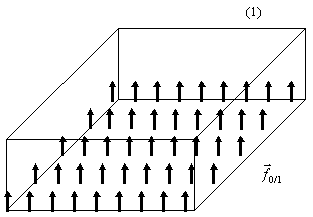
L'action du plan sur la boite peut
être représentée par une force surfacique (force répartie sur
une surface, équivalente à une pression) 
(N.m-2).
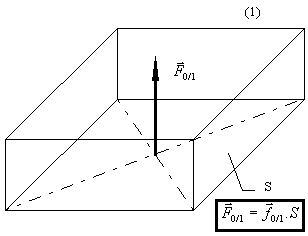
Si la charge est uniforme,
alors l'ensemble de la charge surfacique est équivalente à une
force 
située au centre de la surface de contact.
23-
Actions mécaniques exercées sur des liaisons usuelles parfaites
Une liaison parfaite est une liaison sans frottement.
L'ensemble des actions mécaniques qui s'exercent à l'intérieur d'une liaison peut être représenté par un torseur résultant exprimé au centre de la liaison.[Visualiser les Torseurs]
Le principe de la statique est une application particulière du principe fondamental de la dynamique que nous aborderons dans le chapitre sur la dynamique.
Un solide indéformable en équilibre sous l'action de n actions extérieures reste en équilibre si la somme des torseurs associés à ces actions est égale au torseur nul, soit
 |
 |
| Remarque: · La projection de ces deux relations vectorielles permet d'obtenir six équations dans l'espace et trois équations dans un plan. |
32-
Principe des actions mutuelles
Pour deux solides (0) et (1) en contact, l'action exercée par le solide (1) sur le solide (0) est opposée à l'action exercée par le solide (0) sur le solide (1):
 |
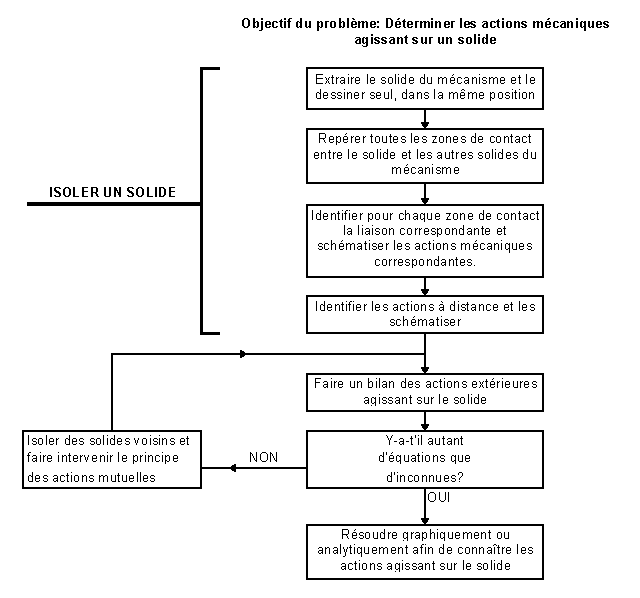
41-
Organigramme de la méthode
421- Solides
soumis à deux forces extérieures
Soit un solide (0) soumis à deux
forces extérieures 
et 
. Soit P le point d'application de la force 
. D'après le
principe de la statique, l'équilibre du solide (0) se traduit
par:
 |
 |
d'où:
| Théorème: Si un solide est en équilibre sous l'action de deux forces extérieures, alors ces deux forces sont égales et opposées. Leur direction passe par les deux points d'application des forces. |
422- Solides
soumis à trois forces extérieures non parallèles
Soit un solide (0) soumis à trois
forces extérieures 
, 
et 
. On suppose parfaitement connues la force ainsi que la
direction de .Soit I le point d'intersection des directions des
forces
et .
D'après le principe de la statique, l'équilibre du solide (0)
se traduit par:
 |
 |
d'où:
Le point I
appartient donc aussi à la direction de
| Théorème:
Un solide soumis à l'action de trois forces extérieures
non parallèles est en équilibre, si: · La somme des trois forces est nulle · Les trois forces sont concourantes en un point. |
423- Solides
soumis à l'action d'au moins quatre forces extérieures
· Cas des forces non coplanaires: Résolution analytique
· Cas des forces coplanaires: Résolution graphique ou analytique
La statique graphique est une méthode de résolution rapide et sans calcul pour les cas plans.
51-
Détermination graphique de la résultante d'un système de
forces
Exemple sur un système de trois forces.
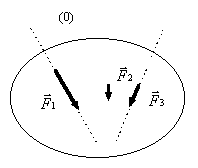
On recherche la résultante des trois forces qui doit vérifier en tous points O de l'espace:
 |
 |
Pour trouver graphiquement la résultante de ces trois forces, on doit tracer un dynamique et un funiculaire.
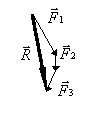
Tracé du dynamique:
Le dynamique permet d'obtenir le tracé de la résultante des trois forces. Il vérifie l'équation:
On connaît alors parfaitement l'intensité et la direction de cette résultante, mais on ignore où cette résultant agit sur le solide (0).
Pour tracer le dynamique, il suffit de mettre bout à bout toutes les forces. On obtient la résultante des forces en partant de l'origine de la première force et en arrivant sur l'extrémité de la dernière .
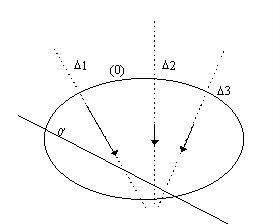
Tracé du funiculaire:
Le funiculaire permet d'obtenir la position de la résultante des trois forces. Il vérifie l'équation:
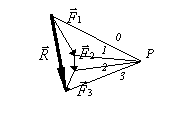
Pour tracer le funiculaire, on commence par tracer sur le dynamique, les rayons polaires. On choisit un point quelconque P appelé pôle et on relie ce point aux extrémités des différents vecteurs. Chaque segment ainsi tracé est un rayon polaire. On les repère par un chiffre.
Le funiculaire est ensuite tracé sur le schéma du solide.
· On trace une parallèle 0' au rayon polaire 0.
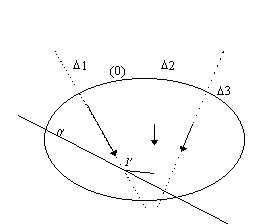
· A l'intersection de 0' et de la direction D 1 de 
, on trace
une parallèle 1' au rayon polaire 1 jusqu'à l'intersection avec
la direction D 2 de 
.
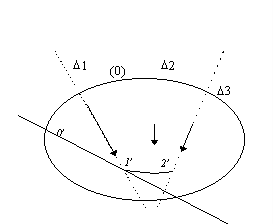
· A l'intersection de 1' et de la direction D 2 de 
, on trace
une parallèle 2' au rayon polaire 2 jusqu'à l'intersection avec
la direction D 3 de. 
.
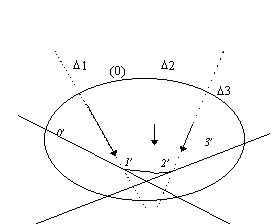
· A l'intersection de 2' et de la direction D 3 de.
.on
trace une parallèle 3' au rayon polaire 3.
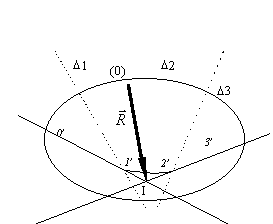
· L'intersection I des droites 0' et 3' est
un point de la droite d'action de la résultante 
.
52-
Equilibre d'un système matériel
521- Equilibre
d'un système matériel soumis à des forces parallèles
Soit un système matériel en
équilibre soumis à trois forces parallèles 
connue, 
et 
inconnues.
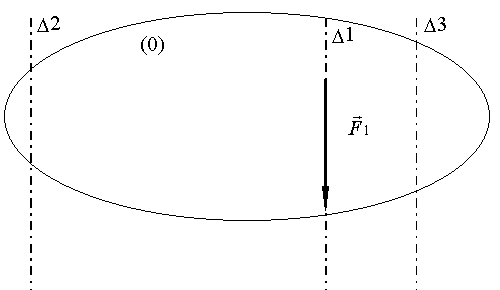
Le système étant en équilibre, les équations suivantes sont vérifiées en tous points O de l'espace:
 |
 |
Pour trouver graphiquement la solution de ce problème, on doit tracer un dynamique et un funiculaire.
Tracé du dynamique:
Le dynamique vérifie l'équation:
Pour tracer le dynamique, il
suffit de tracer la force on voudrait tracer la force au bout de , puis au bout de 
. Le système
étant à l'équilibre, la résultante des trois forces est nulle
et donc l'extrémité de 
correspond à l'origine de .
On dit alors que le dynamique
est fermé. Le problème qui se pose est que l'on ne connaît
pas les intensités de et .
Tracé du funiculaire:
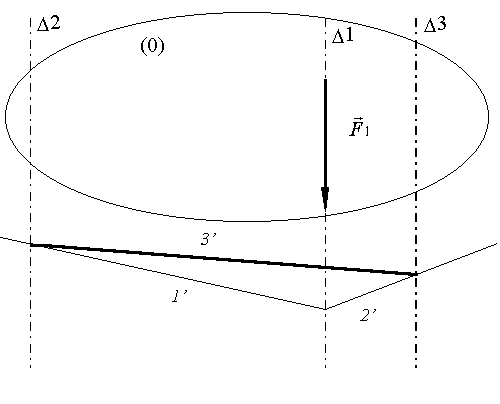
Le funiculaire permet d'obtenir
l’orientation du segment 3’ et donc de déterminer le
rayon polaire 3, correspondant au point de passage de à . On peut
alors en déduire sur le dynamique les intensités de et .
· Le rayon polaire 2 se trouve entre et , on trace
donc le segment 2’ entre les directions D 1 et D 3. Le
rayon polaire 1 se trouve entre et , on trace donc le segment 1’ entre
les directions D 1 et D 2. Le segment 3’, appelé ligne de
fermeture est obtenu en reliant le point d’intersection
de 1’ et D 2, avec le point d’intersection de
2’ et D 3.
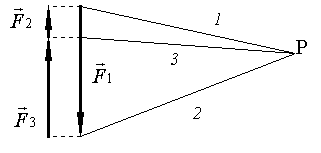· On
reporte alors sur le dynamique, le rayon polaire 3, parallèle à
3’ au point P. On obtient le point correspondant à la
limite des vecteurs et .
.
522- Equilibre
d'un système matériel soumis à des forces concourantes
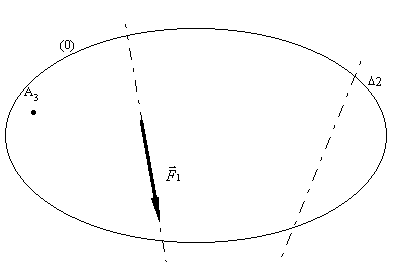
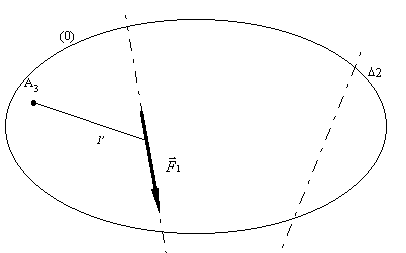
Soit un système matériel en
équilibre soumis à trois forces concourantes , et . Les
inconnues sont l’intensité de ,
l’intensité et la direction de . On connaît
A3, le point d’application de .
Le système étant en équilibre, les équations suivantes sont vérifiées en tous points O de l'espace:
|
 |
De même que dans les paragraphes précédents, on doit tracer un dynamique et un funiculaire.
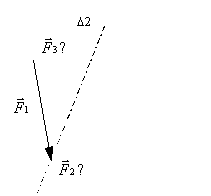
Tracé du dynamique:
Le dynamique vérifie l'équation:
Pour tracer le dynamique, il
suffit de tracer la force . On devrait tracer la force au bout de , puis 
au bout de . Le système
étant à l'équilibre, la résultante des trois forces est nulle
et donc l'extrémité de 
correspond à l'origine de . Le
dynamique est fermé.
Le problème qui se pose est que
l'on ne connaît pas les intensités de et .La direction
de
étant connue, il reste à déterminer le point correspondant à
l'extrémité de et donc à l'origine de .
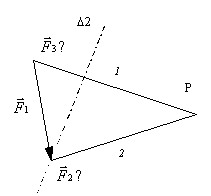
Tracé du funiculaire:
Le funiculaire permet d'obtenir
l’orientation du segment 3’ et donc de déterminer le
rayon polaire 3. On peut alors en déduire sur le dynamique les
intensités de et .· Le rayon polaire 1 se trouve entre et , on trace
donc le segment 1’ entre les directions direction D 3 est
inconnue mais on connaît un point de cette direction: le D 1 et D 3. La
point d'application A3 de .
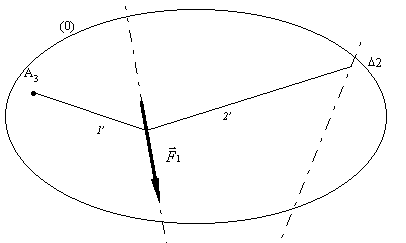
· Le rayon polaire 2 se trouve entre et , on trace
donc le segment 2’ entre les directions D 1 et D 2.
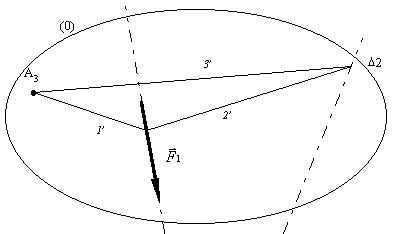
· Le segment 3’, ligne de fermeture, est obtenu en reliant le point A3 au point d’intersection de 2’ et D 2.
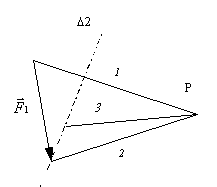
· On reporte alors sur le dynamique, le rayon polaire
3, parallèle à 3’ au point P. On obtient le point
correspondant à la limite des vecteurs et .
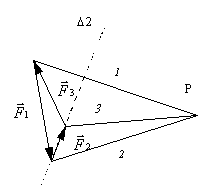
· On peut alors tracer les deux forces et .
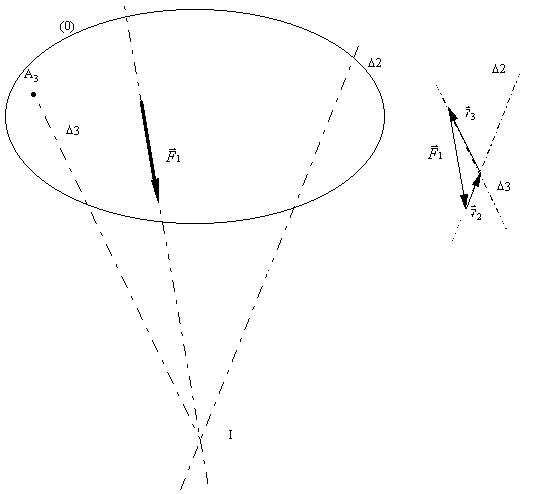
Remarque:
· On peut également résoudre ce problème en
utilisant le théorème d'un solide soumis à trois forces non
parallèles, concourantes en un point. On obtient alors la
direction de qu'il suffit de reporter à l'origine de pour trouver
le point recherché. Cette méthode n’est utilisable que
lorsque le point I de concourance est accessible.
I.S.A. B.T.P.
1, Allée du parc Montaury
64600 ANGLET
tel: 05 59 57 44 29
fax: 05 59 57 44 39
Email: philippe.maron@univ-pau.fr
Mis à jour le: 11/02/04